技術(主にIT技術)について、気が付いたことなどを記録したメモです。
ネットで検索しても出てこないような少し偏った話題を公開するようにしています。
日本語の文書の作成に、pLaTexを使っています。pLaTeXはLaTeXの日本語に拡張したもので、LaTeXはテキストファイル(拡張子"txt")からPDFファイル(拡張子"pdf")を作成するプログラムです。
なお、時代はLaTeXからLuaTeXという新しいプログラムを利用する方向に移行しつつありますが、これまで作ったマクロ(kianマクロ)の修正に莫大な手間がかかるため、現時点では移行できていません。
pLaTeXでは、platexコマンドでテキストファイル(拡張子"txt")からDVIファイル(拡張子"dvi")を生成し、dvipdfmxコマンドでDVIファイル(拡張子"dvi")からPDFファイル(拡張子"pdf")を生成するという2段階を経て、PDFファイルを作成するのが一般的です。
ところで、漢字は全部で10万字を超えるといわれていますが、日常使う字は政府が定めた常用漢字約2000字に限られています。教科書や新聞などは原則として常用漢字のみを使っています。常用漢字はパソコンでそのまま入力でき、pLaTeXでもそのまま使うことができます。
ところが、人の名前についてはこの限りではありません。まず、下の名前(ファーストネーム)は常用漢字に加えて人名用漢字約900字を使うことができます。人名用漢字についてもパソコンでそのまま入力でき、pLaTeXでもそのまま使うことができます。問題は、名字(セカンドネーム)です。
名字はパソコンが普及するずっと前からあり、長い歴史の中で生まれてきたものですので、字体にはたくさんの亜種、すなわち異字体があります。よくあるものでは、「高」と「髙」、「吉」と「𠮷」、「崎」と「﨑」、「浜」と「濵」があります。実は、他にも多量にあり、パソコンで出力する際には、外字を作成したりその文字だけ手書きしたりするなどして、やりくりをしていました。
この問題を解決する取組みが、独立行政法人情報処理推進機構(IPA)が作成したIPAmj明朝フォントです。IPAmj明朝フォントを使うと、異字体を扱うことができます。
https://oku.edu.mie-u.ac.jp/tex/mod/forum/discuss.php?d=917長年、Ubuntu上でRemminaを愛用しています。
Remminaは、いわゆるリモートデスクトップのクライアント環境を提供するもので、簡単に言うと、OS上で別のOSを操作するアプリケーションソフトです。
仮想環境との違いは、仮想環境はコンピュータ上に別の仮想的なコンピュータを起動するのに対し、リモートデスクトップはコンピュータから別の実在するコンピュータを操作する点で違います。
Ubuntu上で、別のWindowsパソコンなどを操作できるわけです。
ところが、突然、横に細い線がたくさん出てきて、昔のアナログ時代の電波の悪いテレビのようになり、事実上、使えなくなりました。先日のvmplayer(VMware Workstation Player)と全く同じ現象です。
試行錯誤した結果、次のようにすれば良いことが判明しました。
「基本設定」タブの「解像度」を「クライアントの解像度を使う」に設定します。これで、横に細い線がたくさん出てくることなく、使えるようになります。
長年、Ubuntu上でvmplayer(VMware Workstation Player)を愛用しています。
vmplayerは、いわゆる仮想環境を提供するもので、簡単に言うと、OS上で別のOSを起動させるアプリケーションソフトです。
vmplayerを使うと、PCにOSをインストールすることなく、最新や時代遅れのOSを起動させ利用することができます。ネットにつながない孤立した環境で使うのであれば、サポートが切れたOSも使うことも可能です。
一度安定した環境を用意すれば、システムやアプリケーションソフトをアップグレードしたら不具合が出たというようなトラブルを避けることも可能です。
本当に素晴らしいソフトで、開発元であるVMware, Incには心からの謝意を表します。
ところが、突然、横に細い線がたくさん出てきて、昔のアナログ時代の電波の悪いテレビのようになり、事実上、使えなくなりました。「The virtual machine could not be changed to the selected monitor layout. If you just added a monitor to the host computer, you must power off and power on the virtual machine to use that monitor」という警告も出ます。
試行錯誤した結果、次のようにすれば良いことが判明しました。
「Virtual Machine」タブの「Virtual Machine Settings」を起動し、「Hardware」タブの「Display」項目の「Accelerate 3D graphics」を有効にします。これで、横に細い線がたくさん出てくることなく、使えるようになります。
ファイルの名前を一時的に変えて、コマンドを実行した後、元に戻したいことがあります。また、ファイルを一時的に別のディレクトリに移動して、そこでコマンドを実行した後、元に戻したいことがあります。
コマンドライン上で、ファイルの名前を一時的に変えてたり、ファイルを一時的に別のディレクトリに移動したりする場合、mvを使って次のように実行します。
> mv file_a file_b
元に戻すときには、次のように実行します。
> mv file_a file_b # ファイルの名前を一時的に変えた場合
> mv file_b/file_a # ファイルを一時的に別のディレクトリに移動した場合
これが手間です。そこで、次のように出来ないかを考えました。
> vm file_a file_b
これならば、履歴のmvをvmに変えるだけで、実行できます。
早速、実装したものが、次のShell Script(シェルスクリプト)です。
#!/bin/sh
# vm
# mvの逆を実行するスクリプト
LANG=C
opt=
for arg; do
test "$arg" = '--' && break
echo "$arg" | grep '^-' > /dev/null || break
opt="$opt $arg"
shift
done
mode='rename'
if [ $# -le 1 ]; then
mode='help'
elif [ $# -le 2 ]; then
bname=`basename $1`
if [ -e "$2/$bname" ]; then
if [ "$2" = '..' ]; then
mode='move'
elif [ "$2" = '.' ]; then
mode='move'
elif ( echo "$2" | grep -e '/$' > /dev/null ); then
mode='move'
else
echo -n "rename \"$2\" to \"$1\"?> "
read answer
test "$answer" = 'y' || mode='move'
fi
fi
else
mode='move'
fi
ret=0
if [ "$mode" = 'help' ]; then
mv $opt -- $@ || ret=1
elif [ "$mode" = 'rename' ]; then
if [ ! -e "$2" ]; then
echo "mv: '$2' does not exist" 1>&2; ret=3
elif [ -e "$1" ]; then
echo "mv: '$1' exists" 1>&2; ret=2
else
mv $opt -- "$2" "$1" || ret=4
fi
else
dir=`eval printf %s \"\\$$#\"`
if [ ! -d "$dir" ]; then
echo "mv: '$dir' is not a directory" 1>&2; ret=5
else
for file; do
bname=`basename "$file"`
if [ ! -e "$dir/$bname" ]; then
echo "mv: '$dir/$bname' does not exist" 1>&2; ret=7
elif [ -e "$file" ]; then
echo "mv: '$file' exists" 1>&2; ret=6
else
mv $opt -- "$dir/$bname" "$file" || ret=8
fi
shift
test $# -eq 1 && break
done
fi
fi
exit $ret
前回は、コマンドのエラー出力をファイルに書き込む話をしました。今回も、コマンドのエラー出力について話したいと思います。
UNIX系のOSでShell(シェル)、すなわちコマンドラインにコマンドを打ち込んでいると、コマンドの出力を編集したい場合があります。
例えば、日時を出力するdateの出力を編集して、来年の今日の今の時刻を取得するには、次のように実行します。">"はコマンドプロンプトですので、入力する必要はありません。
> date +'%Y-%m-%d %H:%M:%S' | sed 's/2021/2022/'
2022-09-01 06:12:34
「2022年9月1日午前6時12分34秒」という出力を得ることができました。
コマンドの出力には、コマンドの実行結果の出力の他にも、エラー出力もあります。ここにいう実行結果の出力とは、コマンドの本来的な出力で、例えばdateであれば日付の出力です。これに対して、エラー出力とは、コマンドのエラーメッセージの出力で、例えばdate --next-yearを実行すると次のような標準エラー出力が得られます。
> date --next-year
date: unrecognized option '--next-year'
Try 'date --help' for more information.
"unrecognized option"、すなわち「'--next-year'なんて知らない」という趣旨のエラー出力が得られました。
このエラー出力を"illeagal option"、すなわち「'--next-year'は違反です」という趣旨のエラー出力に編集することを考えます。あまりないとは思いますが、Shell Script(シェルスクリプト)内で、エラーの書式を統一したい場合には、そういう処理が必要な場合もあるかもしれません。また、既知のエラーについては、出力を抑制したい場合もあるかもしれません。
もちろん、次のようにしてもうまくいきません。なぜならば、パイプ("|")で次のコマンド("sed")に渡されるのは、標準出力だけだからです。
> date --next-year | sed 's/unrecognized/illeagal/'
そこで、実行結果の出力とエラー出力の出力先を入れ換えて編集し、出力先を入れ換えるようにします。具体的には、次のように実行します。
> { { date --next-year 3>&2 2>&1 1>&3; } | sed 's/unrecognized/illeagal/'; } 3>&2 2>&1 1>&3
date: illeagal option '--next-year'
Try 'date --help' for more information.
無事、"unrecognized option"がこれを"illeagal option"に変わりました。"3>&2 2>&1 1>&3"で実行結果の出力とエラー出力の出力先を入れ換えています。
また、中括弧("{"、"}")は、複数のコマンドを1つのコマンドにまとめています。
ただし、このやり方だとコマンドの実行に成功したのか失敗したのかを取得できず、制御ができません。
そこで、コマンドの実行結果で制御する場合には、次のようなShell Script(シェルスクリプト)を組む必要があります。
#!/bin/sh
LANG=C
test_command (){
echo OUT
echo ERR 1>&2
#return 0 # GOOD
return 1 # BAD
}
filter (){
A=`cat`
B=`echo "$A" | head -n -1`
C=`echo "$A" | tail -n 1`
echo "$B" | sed 's/^ERR$/err/'
return `echo "$C" | tail -n 1`
}
{ { test_command 3>&2 2>&1 1>&3; echo $?; } | filter; } 3>&2 2>&1 1>&3 && echo GOOD || echo BAD
"date --next-year"のようなコマンドの代わりに、実験用に"test_command"という関数を使っています。
まず、"echo $?"で一旦、出力にコマンドの戻り値を加えておいて、"filter"で分離し、改めて戻り値にしています。
これで、"test_command"のエラー出力をERRからerrに編集しつつ、"test_command"の実行に成功した場合(""の場合)にはGOODと、失敗した場合にはBADと表示します。
UNIX系のOSでShell(シェル)、すなわちコマンドラインにコマンドを打ち込んでいると、コマンドの実行結果の出力をファイルに書き込みたい場合があります。
その場合、大なり不等号(">")を使って、次のように実行します。なお、行頭の">"はコマンドプロンプトですので、入力する必要はありません。
> command >file
これで、commandの実行結果の出力がfileという名前のファイルに書き込まれます。
この大なり不等号(">")を使って出力先を指定することを、リダイレクトといいます。
ところで、コマンドの出力には、コマンドの実行結果の出力の他にも、エラー出力もあります。エラー出力とは、エラーメッセージの出力で、実行者にエラー発生の事実とその原因を知らせるために出力されるものです。
そのためエラー出力は端末に表示させて読むのが通常ですが、たまにエラー出力を実行結果の出力に含めて出力させたい場合があります。そのような場合には、次のように実行します。
> command 2>&1
"2>&1"で、エラー出力を実行結果と合わせて出力させています。"2"がエラー出力を、"1"が実行結果の出力を意味しています。
それでは、エラー出力をそのまま実行結果の出力と合わせて出力させ、ファイルに書き込みたい場合は、どのように実行すれば良いでしょうか?
よく勘違いするのが、次のような実行例です。
> command 2>&1 >file
これは、大なり不等号(">")の流し込んでいるようなイメージがあるため、"2>&1"でエラー出力を実行結果の出力に流し込み、">file"でエラー出力が合わされた実行結果の出力をファイルに流し込んでいるかのように、勘違いしてしまったためです。
正しくは、リダイレクトの順番を逆にして、次のように実行します。
> command >file 2>&1
まず、">file"は"1>file"を短縮したものですので、この実行例は次と同じです。
> command 1>file 2>&1
コマンドラインは左から評価します。
まず、"command"の時点では、次のようになっています。
標準出力はコマンドの実行結果の出力のデフォルトの出力先、標準エラー出力はコマンドのエラー出力のデフォルトの出力先のことです。
次に、"1>file"によって、1番のコマンドの実行結果の出力先を、ファイル"file"に指定していますので、次のように変化します。
file"最後に、"2>&1"によって、2番のコマンドのエラー出力の出力先を、1番の実行結果の出力先と同じものに指定していますので、次のように変化します。
file"file"その結果、エラー出力は実行結果と合わせて出力され、ファイルに書き込まれるのです。
ちなみに、上の勘違いの例では、最終的に次のようになっています。
file"Shellのリダイレクトの順番は勘違いしやすいけれど、よく考えたら当然ですね。
情報処理安全確保支援士試験を受験しなんとか合格しました。今回は、その受験勉強の際に気が付いたことをお話します。
受験勉強の基本中の基本は、過去の試験問題を解くことです。
そのためには、過去の試験問題と解答を入手する必要があります。試験の実施主体であるIPA(独立行政法人情報処理推進機構)のウェブページには過去の試験問題と解答が載せられているのですが、解答の理由の説明がありません。初学者が解答を見てすぐにその理由が理解できるわけがありませんので、解答の理由の説明を読むために市販の過去の試験問題の問題集(過去問題集)を買うのが、一般的だと思います。
私も過去問題集を購入して使っていたのですが、試験本番3日前、あることに気が付きました。
なんと、過去問題集の解答は、IPAの公式の解答と違っていたのです。そのほとんどは言い回しの違いでしたので、特に問題はありませんでした。
しかし、ごく一部ですが、明らかに出題趣旨を捉えられていないものがありました。
例えば、平成29年春期午後IIの問1の設問6の(3)です。あるマルウェア(ウィルス)に感染したPCは、そうでないPCと何が違うかを、具体的に問う問題です。IPAの解答は、マルウェアが「一通りの処理を終えると自身のファイルの隠蔽処理を行うとともに、自身を所定の時間経過後に起動するための設定をOSに対して組み込み、終了すること」に着目し、「PC起動時や所定の時刻などに特定のプログラムを自動的に起動する設定内容」となっています。ところが、私が購入した過去問題集の解答は、感染したPCがマルウェアを発見できなかったことに着目して、「セキュリティソフトのウィルス定義ファイル」という趣旨のことが書かれていました。
問題文の前後の文脈から、出題趣旨がマルウェアの特徴を踏まえた違いにあることは明白で、私が購入した過去問題集の解答は出題趣旨を完全に外しています。ここまで極端ではないにしても、他にも違和感のある解答がいくつかありました。
IPAは公式の解答を発表していますので、過去問題集の解答も公式の解答を使い、それに理由の説明を付け加えているものだと、勝手に思っていました。
情報処理安全確保支援士試験の勉強される方は、過去問題集の解答だけではなく、IPAの公式の解答を確認することをお勧めします。
電子データを手渡す際に、光学ディスク(CD-R、DVD-R、BD-R)を使うことがあります。
光学ディスクでは、ISO 9660という光ディスクに特化したファイルシステムを使ったイメージファイルを作成し、それをディスクに焼き付けるのが一般的です(もちろん、別のファイルシステムを使ったり、イメージファイルを作成しながらディスクに焼き付けたりすることもできます。)。
ISO 9660のイメージファイルを作る際には、UNIX系のOS(FreeBSD、Linuxなど)ではmkisofsというコマンドを使い、例えばdataというディレクトリの中にファイルを集め、次のように実行します。">"はコマンドプロンプトですので、入力する必要はありません。
> mkisofs -o data.iso data
これで、data.isoという名前でとりあえずはイメージファイルができます。
しかし、ISO 9660は1988年に制定された非常に古い規格であるため、デフォルトではファイル名は8文字までで漢字などの全角文字が使えないなど極めて厳しい制限があり、現実的な使用は難しいです。
そこで、オプションで拡張機能を追加するのですが、そのオプションを毎回忘れるので、今回はそのメモです(ちなみに、出力するイメージファイル名を指定するオプション"-o"もよく忘れて、エラーになります。)。
まず"-J"というオプションです。これは、Joliet拡張と呼ばれるもので、ファイル名を拡張するものです。Windowsのために開発された拡張で、Windowsで使用する場合には、事実上必須です。上位互換性があるので、この拡張に対応していないシステムでも、拡張を除いて普通に利用できます。
次に"-r"というオプションです。これは、Rock Ridge拡張と呼ばれるもので、ファイル名を拡張しファイルの所有者や権限も記録するものです。ファイル名の大文字と小文字も区別してくれます。UNIX系のOSのために開発された拡張です。上位互換性があるので、この拡張に対応していないシステムでも、拡張を除いて普通に利用できます。なお、Rock Ridge拡張には"-R"というオプションもあり、こちらは所有者をそのまま記録するものですが、バックアップを取るときを除いて、通常、ファイルの所有者をそのまま記録する必要はありませんので、"-r"で十分だと思います。
さらに"-g"というオプションもあります。これは、アップルが当時のMacのために開発したいくつかの拡張を付けるものです。ただし、上位互換性が不完全ですし、最近のMacはJoliot拡張やRock Ridge拡張に対応していますので、使用するメリットがあまりありません。
これらをまとめると、mkiosfsは、Joliot拡張とRock Ridge拡張を付けて、次のように実行するのが良いと思います。
> mkisofs -J -r -o data.iso data
ファイル名が長い場合には、Joliot拡張の限界を越えてしまい、イメージファイルを作成できないことがあります。その場合には、Joliot拡張の規格に反しますのであまりおすすめしませんが、"-joliet-long"をつけてやると、作成できる場合があります。ハイパーテキストなどでリンクが張られていて、別の名前に変えてしまうと、リンク先を閲覧できなくなってしまうような場合には、規格に反していても使わざるを得ないと思います。
> mkisofs -joliet-long -r -o data.iso data
前回は、MetaPostで画像に日本語を書き込む場合、upmpostを使うという話をしました。
あとから日本語を書き込んでも良いのであれば、MetaPost等で画像だけを作っておいて、ImageMagickで日本語を後から書き込むという方法もあります。今回はその方法をご説明いたします。この方がフォントもたくさん使えて便利かもしれません。
まず、次のコマンドで使用することができるフォントを探します。なお、ImageMagickはアプリケーション名とコマンド名が全く違う珍しいアプリケーションで、convertはImageMagickのコマンドです。また、">"はコマンドプロンプトですので、入力する必要はありません。
> convert -list font
なお、
試しに、IPAフォントを探してみます。
> convert -list font | grep -A 4 IPA
Font: IPA-Pゴシック
family: IPA Pゴシック
style: Normal
stretch: Normal
weight: 400
glyphs: /usr/share/fonts/opentype/ipafont-gothic/ipagp.ttf
Font: IPA-P明朝
family: IPA P明朝
style: Normal
stretch: Normal
weight: 400
glyphs: /usr/share/fonts/opentype/ipafont-mincho/ipamp.ttf
Font: IPAexゴシック
family: IPAexゴシック
style: Normal
stretch: Normal
weight: 400
glyphs: /usr/share/fonts/opentype/ipaexfont-gothic/ipaexg.ttf
Font: IPAex明朝
family: IPAex明朝
style: Normal
stretch: Normal
weight: 400
glyphs: /usr/share/fonts/truetype/fonts-japanese-mincho.ttf
Font: IPAゴシック
family: IPAゴシック
style: Normal
stretch: Normal
weight: 400
glyphs: /usr/share/fonts/opentype/ipafont-gothic/ipag.ttf
Font: IPA明朝
family: IPA明朝
style: Normal
stretch: Normal
weight: 400
glyphs: /usr/share/fonts/opentype/ipafont-mincho/ipam.ttf
結果はシステムによって違うと思いますが、私のパソコンでは上記のような結果になりました。glyphsのパスを見ていただければ分かると思いますが、原則としてOSにインストールされている全てのフォントが使えます。
フォントの違いについて、少しご説明しておきます。
「明朝」は明朝体のことで、縦横で太さを変えたシャープな印象のフォント、「ゴシック」はゴシック体のことで、均一の太さで書かれた優しい印象のフォントです。
「IPA-P明朝」と「IPA-Pゴシック」はプロポーショナルフォントと呼ばれているフォントで、文字によって幅が違うフォントです。ブラウザやファイラなど限られた幅の中に出来るだけ情報を詰め込みたいときに使います。
「IPA明朝」と「IPAゴシック」は日本語は等幅フォントと呼ばれるフォントで、全角文字(漢字等)は幅2、半角文字(アルファベットや数字)は幅1に固定したフォントです。タイプライターで書いた文書のように、均一な文字幅で書きたいときに使います。
「IPAex明朝」と「IPAexゴシック」は、全角文字は等幅フォント、半角文字はプロポーショナルフォントで作られたフォントです。漢字は等幅で書き、アルファベットはプロポーショナルで書くのが、一般的に美しいと言われていますので、合理的だと思います。
今回は「IPAex明朝」と「IPAexゴシック」を使って、前回と同じような画像を作ります。
まず、白紙の画像を作ります。これは何で作っても構いません。前回ご紹介したMetaPostでも作れますし、GIMPでも作れます。Windows上であれば、Microsoft Paintでも作れます。今回は、せっかくなのでImageMagickで作ってみます。
> convert -size 360x70 xc:white convert-white.png
これで、横360、縦70の白紙の画像"convert-white.png"が出来ました。
これに明朝とゴシックで「日本語」と書き込みます。コマンドのオプションが長いので、改行を入れてあります。また、文字に色を付けたい場合を考えて、今回は文字を青にしました。
> convert -gravity southwest -pointsize 50 -stroke blue \
-font IPAex明朝 -annotate +10+10 '日本語' convert-white.png convert-temp.png
> convert -gravity southwest -pointsize 50 -stroke blue \
-font IPAexゴシック -annotate +190+10 '日本語' convert-temp.png convert-char.png
"-gravity southwest"で座標の原点の位置を、"-pointsize 50"で文字の大きさを、"-stroke blue"で文字の色を、"-annotate +10+10"及び"-annotate +190+10"で文字を書き込む位置を指定しています。
先の例では、分かりやすいように明朝体とゴシック体の2段階に分けて書き込みましたが、1段階で書き込むことも出来ます。
> convert -gravity southwest -pointsize 50 -stroke blue \
-font IPAex明朝 -annotate +10+10 '日本語' \
-font IPAexゴシック -annotate +190+10 '日本語' \
convert-white.png convert-char.png
出来上がったのは次の画像です。

ImageMagickは、メモリをたくさん使う、処理速度が遅い、脆弱性が報告されているという欠点もありますが、ほとんど全てのファイル形式に対応してる、細かい指定が可能で融通が利くという利点があり、気を付けて使えば非常に便利なアプリケーションです。
元々、MetaPostはmpostというコマンドで、labelに日本語は使えませんでしたので、画像に日本語を書き込むことはできませんでした。
> mpost ascii.mp
そのうち、jmpostというコマンドが作られ、labelに日本語が使えるようになりました。"j"は"Japanese"の頭文字だと思います。
例えば、次のようなファイルから日本語が書き込まれた画像を作成できるようになりました。なお、"rml"は明朝体で、"gbm"はゴシック体の設定です。
% MetaPost
prologues := 3;
beginfig(-1);
fill (0,0)--(360,0)--(360,70)--(0,70)--cycle withcolor white;
label.bot("日本語" infont "rml" scaled 5,(90,60));
label.bot("日本語" infont "gbm" scaled 5,(270,60));
endfig;
end.
これを文字コード"euc"で、"euc-rml+gbm.mp"という名前で保存し、次を実行します。なお、当たり前ですが、文字コードが違えば確実に文字化けしますので、文字コードには細心の注意が必要です。
> jmpost euc-rml+gbm.mp
> convert euc-rml+gbm.ps euc-rml+gbm.png
すると、次のような日本語が書き込まれた画像を作成できました。

ところが、jmpostはいつの間にやらパッケージシステムからなくなってしまいました。
これはmpostが国際化されて日本語が使えるようなったのではないかと、勝手に思い込みました。
そこで、文字コードを"utf-8"に変換して、mpostを実行してみました。
> nfk -w euc-rml+gbm.mp > utf8-rml+gbm.mp
> mpost utf8-rml+gbm.mp
残念ながら、これはエラーで実行できませんでした。
仕方なく、その後何年もjmpostを無理矢理に使い続けてきました(無理矢理に使う方法は、別の機会にご説明したいと思います。)。
前回の記事を書くに当たって、久しぶりにMetaPostを"texlive-metapost"といパッケージからインストールしてみましたが、やはりmpostはうまく実行できませんでした。
しかし、何かの拍子にupmpostというコマンドを発見しました。直感的に"up"は国際的文字コードを意味する"Unicode"の頭文字と歴史的に日本語拡張を意味する"Publishing"の頭文字ではないかと思いました。
そこで、upmpostを実行してみました。
> upmpost utf8-rml+gbm.mp
> convert -type GrayScale utf8-rml+gbm.ps utf8-rml+gbm.png
エラーになることなく、正常に実行できました。
しかし、出来上がった画像は次のとおりです。

文字化けしていて全く読めません。
しかし、これは大きなヒントになりました。正常に実行できるけれど、文字化けするということは、フォントの設定が悪いということです。
そこで、フォントが入っているディレクトリ(/usr/share/texlive/texmf-dist/fonts/tfm)の下を探したところ、同じように"up"が頭につくuptex-fontsというディレクトリの下に"urml.tfm"と"ugbm.tfm"というファイルを発見しました。これを使うと良さそうです。
早速、"rml"を"urml"に、"gbm"を"ugbm"に書き換えて、文字コード"utf-8"で、"utf8-urml+ugbm.mp"という名前で保存します。
% MetaPost
prologues := 3;
beginfig(-1);
fill (0,0)--(360,0)--(360,70)--(0,70)--cycle withcolor white;
label.bot("日本語" infont "urml" scaled 5,(90,60));
label.bot("日本語" infont "ugbm" scaled 5,(270,60));
endfig;
end.
upmpostを実行します。
> upmpost utf8-urml+ugbm.mp
> convert -type GrayScale utf8-urml+ugbm.ps utf8-urml+ugbm.png
出来上がった画像は次のとおりです。

まとめると、MetaPostのコマンドは日本語を使う場合はupmpostで、フォントは"urml"(明朝体)と"ugbm"(ゴシック体)を使えば良いということが分かりました。
文章を書いていると、説明を分かりやすくするため、絵が欲しいときがあります。そのようなときは、MetaPostを使って、絵を描いています。
このページのロゴ「梅星(うめぼし)」もMetaPostを使って書きました。

余談ですが、このロゴはその名前のとおり、形は冬の寒さに越えて早春に咲く梅の花を、色は重力収縮により光り始めた原始星を表しています。いずれも新たな時の始まりを告げる息吹をイメージしています。
話を元に戻しますが、MetaPostはプログラムコードから絵を作るアプリケーションソフトです。説明を分かりやすくするための絵に必要なのは芸術性ではなく論理性ですから、お絵書きソフトで描くよりもプログラムコードから描いた方が論理的で分かりやすく作ることができますし、描いた絵の修正や再利用も容易だからです。
ところが、絵が欲しい頻度が年に1回程度のため、毎回、文法をすっかり忘れてしまっていて、これまではネットで検索して勉強し直しながら描いていました。先日も絵が欲しいことがあったのですが、時間をかけて勉強し直しました。あまりに効率が悪いので、これを機にメモを残しておきます。
% metapost.mp
% MetaPostの書き方のメモ
% おまじない
prologues := 3;
beginfig(-1);
%=====================================%
% 用紙
lx = 450;
ly = 450;
path canvas;
canvas = (0,0)--(lx,0)--(lx,ly)--(0,ly)--cycle;
fill canvas withcolor white;
%=====================================%
% 変数
numeric n;
n = 10;
pair p;
p = (0,0);
path P;
P = (0,0)--(1,1);
%=====================================%
% ペン
pickup pencircle scaled 2;
% pickup pensquare scaled 2;
%=====================================%
% 文字の大きさ
defaultscale:=1.2;
%=====================================%
% 四角形
label.bot("0",(075,045));
draw (050,050)--(100,050)--(100,100)--(050,100)--cycle;
%=====================================%
% 円
label.bot("1",(175,045));
draw (175,50)..(200,75)..(175,100)..(150,75)..cycle;
%=====================================%
% べた
label.bot("2",(275,045));
fill (250,050)--(300,050)--(300,100)--(250,100)--cycle;
%=====================================%
% 色
label.bot("3",(375,045));
fill (350,050)--(400,050)--(400,100)--(350,100)--cycle withcolor .75red+.50green+.25blue;
%=====================================%
% 並進
label.bot("4",(075,145));
path P;
P = (00,00)--(50,00)--(50,50)--(00,50)--cycle;
pair p;
p = (50,150);
draw P shifted(p);
%=====================================%
% 回転
label.bot("5",(175,145));
path P;
P = (-18,-18)--(+18,-18)--(+18,+18)--(-18,+18)--cycle;
draw P rotated(45) shifted((175,175));
%=====================================%
% 文字
label.bot("6",(275,145));
draw (260,160)--(290,160)--(290,190)--(260,190)--cycle withcolor black;
label.ulft("TL",(260,190)); % 上左
label.top("TC",(275,190)); % 上中
label.urt("TR",(290,190)); % 上右
label.lft("CL",(260,175)); % 中左
label.rt("CR",(290,175)); % 中右
label.llft("BL",(260,160)); % 下左
label.bot("BC",(275,160)); % 下中
label.lrt("BR",(290,160)); % 下右
%=====================================%
% 線が出る方向
label.bot("7",(375,145));
draw (350,150){1,0}..(400,175)..{-1,0}(350,200)--cycle;
%=====================================%
% 関数
label.bot("8",(075,245));
def func(expr a, t, c) =
path P;
P = (-18,-18)--(+18,-18)--(+18,+18)--(-18,+18)--cycle;
fill P rotated(a) shifted(t) withcolor c;
enddef;
func(45, (075,275), .25red+.50green+.75blue);
%=====================================%
% 破線
label.bot("9",(175,245));
draw (150,250)--(200,250)--(200,300)--(150,300)--cycle dashed evenly;
%=====================================%
% 点線
label.bot("A",(275,245));
draw (250,250)--(300,250)--(300,300)--(250,300)--cycle dashed withdots;
%=====================================%
% ペンの変更
label.bot("B",(375,245));
draw (350,250)--(400,250)--(400,300)--(350,300)--cycle withpen pencircle scaled 2;
%=====================================%
% 矢印
label.bot("C",(075,345));
drawarrow (050,350)--(100,400);
drawarrow (050,400)--(100,350);
%=====================================%
% 点
label.bot("D",(175,345));
draw (155,355) withpen pencircle scaled 10; % 丸点
draw (195,395) withpen pencircle scaled 10; % 丸点
draw (155,395) withpen pensquare scaled 10; % 角点
draw (195,355) withpen pensquare scaled 10; % 角点
%=====================================%
% 日本語
label.bot("E",(275,345));
% /usr/share/texlive/texmf-dist/fonts/tfm/uptex-fonts/
label.top("漢字" infont "urml" scaled 2.2,(275,375)); % 明朝
label.bot("漢字" infont "ugbm" scaled 2.2,(275,375)); % ゴシック
%=====================================%
%
label.bot("F",(375,345));
endfig;
end.
このコードを"metapost.mp"という名前で保存し、次のように実行します。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> upmpost metapost.mp
これで、次のような絵が、"metapost.ps"という名前のPostScriptファイルで出来上がります。
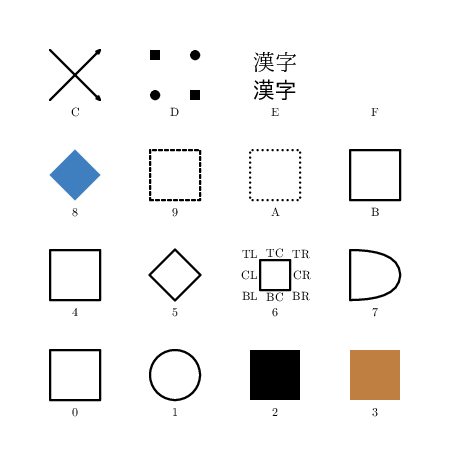
これは、次のようなTeXのコードで文章に取り込むことができます。
% metapost.tex
% 絵を取り込むためのサンプルコード
\documentclass[a4paper,papersize,12pt]{jsarticle}
\usepackage{graphicx}
\begin{document}
\fbox{\includegraphics[scale=.8]{metapost.ps}}
\end{document}
これを"metapost.ps"のあるディレクトリで"metapost.tex"という名前で保存し、次のように実行すると"metapost.pdf"が生成されますので、一般的なPDFビューアで見ることができます。
> platex metapost.tex
> dvipdfmx metapost.dvi
TeX以外で利用するのであれば、ImageMagickを使ってpng又はjpgに変換すれば、一般的な画像ビューアで見ることができるようになりますし、HTMLにも取り込むことができるようになります。
> convert metapost.ps metapost.png
> convert metapost.ps metapost.jpg
前回に引き続き、Shell Script(シェルスクリプト)のお話です。
Shell Scriptを書いていると、編集途中のデータを一時的に保存する場合など、一時ディレクトリを作成しその中で作業したい場合があります。
作業が終わると一時ディレクトリを消去することになりますが、その消去は危険なので注意が必要です。
一時ディレクトリを使うの典型例は、次のようなものです。
#!/bin/sh
# 一時ディレクトリを使うの典型例
tmpdir=/tmp/foo # 一時ディレクトリを定義
mkdir $tmpdir # 一時ディレクトリを作成
...
bar ... > $tmpdir/tmpfile.txt # 一時ディレクトリを利用
...
rm -rf $tmpdir # 一時ディレクトリを消去
最後の行で、一時ディレクトリを消去しています。しかし、$tmpdirが"/tmp/foo"のままである保証はどこにあるでしょうか。一般的なShellには、定数という概念がないため、変数はいつでも代入して、変更できてしまいます。そのため、もしコードにバグがあって、$tmpdirが"/"が代入されていたら、システム全体を消去し破壊してしまう可能性があります。
なお、コードの中のディレクトリ名の"foo"とコマンドの"bar"は、メタ構文変数と呼ばれるもので、意味のない名前です。日本語の文章に使われる"〇〇"のようなもので、特に意味はありません。
一般的に、変数やワイルドカードで指定して、ファイルやディレクトリを消去することはとても危険です。
例えば、次のコードは非常に危険です。
rm -rf $tmpdir/* # 一時ディレクトリ内の全ファイルとディレクトリを消去
もし$tmpdirが空文字列であったら、"rm -rf /*"を実行し、システム全体を消去し破壊してしまいます。$tmpdirがたまたま"/"に変わっていることはあまり考えられませんが、代入のミスや定義の欠如によって$tmpdirが空文字列であることは十分に考えられます(一般的なShellは、定義のない変数をエラーにせず、空文字列として扱うため、定義の欠如でもシステム全体を消去し破壊してしまいます。)。
はるか昔の学生時代のことですが、重要なファイルのバックアップを取るShell Scriptを書いた際に、その中に上記のようなコードを書いてしまっておりました。そして、コードを修正した際にバグが入り込み、$tmpdirが空文字列を代入してしまい、システム全体を消去してしまった経験があります。重要なファイルをバックアップしようとして、そのファイルはもちろん、そのファイルのバックアップも含めてシステム全体を消去してしまうという本末転倒の笑えない結果になってしまいました。
一時ディレクトリは、固定文字列を付け足して、次のような使い方をした方が安全です。
#!/bin/sh
# 一時ディレクトリの安全な使い方
tmpdir=/tmp/foo # 一時ディレクトリの親ディレクトリを定義
mkdir -p $tmpdir/ectory # 一時ディレクトリを作成
...
bar ... > $tmpdir/ectory/tmpfile.txt # 一時ディレクトリを利用
...
rm -rf $tmpdir/ectory # 一時ディレクトリを消去
rmdir $tmpdir # 一時ディレクトリの親ディレクトリを消去
このような使い方をしていれば、仮に$tmpdirの値が変わっていたり空文字列になっていたりしたとしても、たまたまその下に"ectory"という名前のファイルやディレクトリがなければ、何も消去しません。
もっとも、一時ディレクトリを使うたびに、このような神経を使った書き方をするのは面倒です。そこで、私は、次のような関数を作成して使っています。
#!/bin/sh
# tmpdir.sh
# 一時ディレクトリを安全に作成し消去する関数
mktmpdir (){
(
test $# -le 1 || return 1
_b=`basename $0`; test -n "$_b" || return 2
test -n "$USER" || return 3
test -n "$$" || return 4
if [ $# -eq 1 ]; then
_r="$*"
else
_r='/tmp'
fi
_t="$_r/$_b-$USER"
test -d "$_r" || return 5
mkdir -p "$_t-tmp/$$" || return 6
chmod 700 "$_t-tmp" "$_t-tmp/$$" || return 7
printf %s "$_t-tmp/$$" || return 8
return 0
)
}
rmtmpdir (){
(
test $# -le 1 || return 1
_b=`basename $0`; test -n "$_b" || return 2
test -n "$USER" || return 3
test -n "$$" || return 4
if [ $# -eq 1 ]; then
printf %s "$*" | grep "/$_b-$USER-tmp/$$/*$" > /dev/null || return 5
_r=`printf %s "$*" | sed "s;/$_b-$USER-tmp/$$/*$;;"`
else
_r='/tmp'
fi
_t="$_r/$_b-$USER"
test -d "$_t-tmp/$$" || return 6
chmod -R 700 "$_t-tmp/$$" || return 7
rm -rf "$_t-tmp/$$" || return 8
ls "$_t-tmp" | while read i; do
ps -p $i > /dev/null || rm -rf "$_t-tmp/$i" || return 9
done
test -n "`ls \"$_t-tmp\"`" || rmdir "$_t-tmp" || return 10
return 0
)
}
# 実行結果の表示
tmpdir=`mktmpdir`
trap "rmtmpdir \"$tmpdir\"; exit 1" INT TERM
echo '# maked tmpdir'
test -d $tmpdir && ls -d $tmpdir || echo '(no such dir)'
echo 'test' > $tmpdir/tmpfile.txt # 一時ディレクトリを利用
rmtmpdir "$tmpdir"
echo '# removed tmpdir'
test -d $tmpdir && ls -d $tmpdir || echo '(no such dir)'
このScriptを"tmpdir.sh"という名前で保存し、実行権限を与えて実行すると、次のような実行結果が得られます("user"という部分と"123456"という部分は実行環境によって異なります。)。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> tmpdir.sh
# maked tmpdir
/tmp/tmpdir.sh-user-tmp/123456
# removed tmpdir
(no such dir)
オブジェクト指向において、変数の代入や取得にはsetメソッドやgetメソッドを使い、変数に直接アクセスしないようにします。それと同じように、わたしは、Shell Scriptにおいて、一時ディレクトリの作成や消去にmktmpdir関数やrmtmpdir関数を使い、一時ディレクトリを直接作成したり消去したりしないようにしています。
なお、一時ディレクトリ名の定義に"-tmp"を含めておりませんが、これはさきほどの"ectory"と同じ意図です。仮に$_tの値が変わっていたり空文字列になっていたりしたとしても、名前が"-tmp"で終わるファイル又はディレクトリがなければ、何も消去しません。仮に名前が"-tmp"で終わるファイル又はディレクトリがあったとしても、その名前から一時ファイル又はディレクトリと予想されますので、致命的な被害にならない可能性が残ります。
また、以前はmktempというコマンドを使ってランダムなディレクトリ名にしていたのですが、現在はプロセスIDをディレクトリ名にして、別の機会に作成されて使用済みになっている一時ディレクトリも消去するようにしています。
実行結果の表示の中のtrapを実行する行(最後から6行目)は、強制終了の場合に一時ディレクトリを消去するためのコードです。一時ディレクトリの作成とセットで実行すべきですので、忘れないように入れておきました。
なお、当たり前ですが、変数やワイルドカードを使って、一時ディレクトリの中を削除してはいけません。個別のファイル名やディレクトリ名を指定して削除するか、rmtmpdirを使って一時ディレクトリ自体を消去するようにします。
> rm -rf $tmpdir/$foo (← ダメ)
> rm -rf $tmpdir/* (← ダメ)
> rm -rf $tmpdir/bar (← よい)
> rmtmpdir $tmpdir (← よい)
たくさんの方に参考にしていただけますと幸いです。
複雑な処理をせず実行速度を気にしないのであれば、プログラムはShell Script(シェルスクリプト)で書くべきだと思います。シンプルに書けますし、汎用性が高いからです。
Shell Scriptでプログラムを書いていて、オプションを受け取りたいときがあります。そのような場合、getoptsというコマンドで、オプション解析ができます。
ショートオプション("-h"のような1文字で表現されるオプション)のみを受け取るのであれば、次のようなScriptで簡単にできます。
#!/bin/sh
# getopts-shortopt.sh
# ショートオプションのみを受け取るShell Script
is_aaa='False'
is_bbb='False'
ddd_val=
eee_val=
while getopts abd:e: OPTNAM; do
case $OPTNAM in
a) is_aaa='True';;
b) is_bbb='True';;
d) ddd_val="$OPTARG";;
e) eee_val="$OPTARG";;
*) exit 1;;
esac
done
shift `expr $OPTIND - 1`
# 実行結果の表示
test "$is_aaa" = 'True' && echo "is_aaa: $is_aaa"
test "$is_bbb" = 'True' && echo "is_bbb: $is_bbb"
test -n "$ddd_val" && echo "ddd_val: $ddd_val"
test -n "$eee_val" && echo "eee_val: $eee_val"
test -n "$*" && echo "rest_args: $*"
getoptsの後の"abd:e:"でオプションを定義し、"case"内でオプションの処理をしています。オプションの定義のコロン(":")は、オプションが引数を取るという意味です。このScriptは、引数を取らない"-a"と"-b"、引数を取る"-d"と"-e"をオプションに持っています。
このScriptを" getopts-shortopt.sh"という名前で保存し、実行権限を与えて実行すると、次のような実行結果が得られます。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> chmod +x getopts-shortopt.sh
> ./getopts-shortopt.sh
> ./getopts-shortopt.sh -a
is_aaa: True
> ./getopts-shortopt.sh -d 100
ddd_val: 100
> ./getopts-shortopt.sh -d
No arg for -d option
> ./getopts-shortopt.sh -x
Illegal option -x
> ./getopts-shortopt.sh zzz
rest_args: zzz
しかし、オプションの数が増えるに従って、文字が被るようになってきます。例えば、"header"、"high-xxx"、"half-xxx"は、いずれも頭文字が"h"ですので"-h"を使いたいところですが、"-h"は一般的に"help"です。
このような場合には、二重ハイフンから始まるロングオプション("--help"、"--header"のような単語で表現されるオプション)を使うと便利です。
ところが、getoptsはロングオプションを解析するように作られていません。そこで、ちょっとした工夫が必要になります。
その工夫を実装したのが、次のScriptです。
#!/bin/sh
# getopts-longopt.sh
# ロングオプションも受け取るShell Script(簡易版)
is_aaa='False'
is_bbb='False'
is_ccc='False'
ddd_val=
eee_val=
fff_val=
while getopts "abd:e:-:" OPTNAM; do
if [ "$OPTNAM" = '-' ]; then
if [ -n "`echo \"$OPTARG\" | grep '='`" ]; then
# --option=argument
OPTNAM=${OPTARG%=*}
OPTARG=${OPTARG#*=}
elif [ -n "`echo \"$OPTARG\" | grep -E \"^eee|fff$\"`" ]; then
# --option argument
OPTNAM=$OPTARG
if [ $OPTIND -gt $# ]; then
echo "No arg for --$OPTNAM option" 1>&2
exit 1
fi
OPTARG=`eval echo \\$$OPTIND`
OPTIND=`expr $OPTIND + 1`
else
# --option
OPTNAM=$OPTARG
OPTARG=
fi
# CHECK
if [ -z "`echo \"$OPTNAM\" | grep -E \"^bbb|ccc|eee|fff$\"`" ]; then
echo "Illegal option --$OPTNAM" 1>&2
exit 1
fi
fi
case "$OPTNAM" in
a) is_aaa='True';;
b|bbb) is_bbb='True';;
ccc) is_ccc='True';;
d) ddd_val="$OPTARG";;
e|eee) eee_val="$OPTARG";;
fff) fff_val="$OPTARG";;
*) exit 1;;
esac
done
shift `expr $OPTIND - 1`
# 実行結果の表示
test "$is_aaa" = 'True' && echo "is_aaa: $is_aaa"
test "$is_bbb" = 'True' && echo "is_bbb: $is_bbb"
test "$is_ccc" = 'True' && echo "is_ccc: $is_ccc"
test -n "$ddd_val" && echo "ddd_val: $ddd_val"
test -n "$eee_val" && echo "eee_val: $eee_val"
test -n "$fff_val" && echo "fff_val: $fff_val"
test -n "$*" && echo "rest_args: $*"
このScriptは、前のScriptの"-b"に"--bbb"というロングオプションを付け加え、引数を取らない"--ccc"というロングオプションを新たに加え、前のScriptの"-e"に"--eee"というロングオプションを付け加え、引数を取る"--fff"というロングオプションを新たに加えました。
これを" getopts-longopt.sh"という名前で保存し、実行権限を与えて実行すると、次のような実行結果が得られます。
> chmod +x getopts-longopt.sh
> ./getopts-longopt.sh
> ./getopts-longopt.sh -a
is_aaa: True
> ./getopts-longopt.sh --bbb
is_bbb: True
> ./getopts-longopt.sh -d 100
ddd_val: 100
> ./getopts-longopt.sh -d
No arg for -d option
> ./getopts-longopt.sh --eee 100
eee_val: 100
> ./getopts-longopt.sh --eee=100
eee_val: 100
> ./getopts-longopt.sh --eee
No arg for --eee option
> ./getopts-longopt.sh -x
Illegal option -x
> ./getopts-longopt.sh --yyy
Illegal option --yyy
> ./getopts-longopt.sh zzz
rest_args: zzz
引数が必要なロングオプションには、"--option value"というタイプと"--option=value"というタイプの2種類がありますが、いずれのタイプにも対応しています(個人的には、ショートオプションとの整合性を考えると、前者の記法が良いとは思っています。)。
これで十分なのですが、新しいオプションを追加する場合に修正すべき場所がたくさんあり、バグの原因になりそうなのが気になります。
そこで、オプションに関する設定を括り出し、実際にversionとhelpを付け加えてみました。
#!/bin/sh
# ロングオプションも受け取るShell Script(実用版)
PROGRAM='foo'
VERSION='v01'
HELP="Usage: $PROGRAM [option] <argument>
Options:
-a set aaa to True
-b, --bbb set bbb to True
--ccc set ccc to True
-d <value> set ddd to <value>
-e, --eee <value> set eee to <value>
--fff <value> set fff to <value>
-v, --version show version number and exit
-h, --help show this message and exit"
# OPTS="$OPTS;x|xxx:"
# x = ショートオプション
# xxx = ロングオプション
# : = 引数をとる場合に指定
# is_xxx='False' / xxx_val=
# 初期値の設定
# opt_xxx (){ is_xxx='True'; } / opt_xxx (){ val_xxx="$OPTARG"; }
# オプションを指定した場合の処理
OPTS=
OPTS="$OPTS;a"; is_aaa='False'; opt_aaa (){ is_aaa='True'; }
OPTS="$OPTS;b|bbb"; is_bbb='False'; opt_bbb (){ is_bbb='True'; }
OPTS="$OPTS;ccc"; is_ccc='False'; opt_ccc (){ is_ccc='True'; }
OPTS="$OPTS;d:"; val_ddd=; opt_ddd (){ val_ddd="$OPTARG"; }
OPTS="$OPTS;e|eee:"; val_eee=; opt_eee (){ val_eee="$OPTARG"; }
OPTS="$OPTS;fff:"; val_fff=; opt_fff (){ val_fff="$OPTARG"; }
OPTS="$OPTS;v|version"; print_version (){ echo "$PROGRAM $VERSION"; exit 0; }
OPTS="$OPTS;h|help"; print_help (){ echo "$HELP"; exit 0; }
# sopts='abc:d:'
sopts=`echo "$OPTS" | sed -e 's/|\?[^|:;]\{2,\}//g' -e 's/;:\?//g'`
# lopts='|aaa|bbb|ddd:|eee:|'
lopts=`echo "$OPTS;" | sed -e "s/;/;;/g" -e 's/;[^|:;][|:;]//g' -e 's/;\+:\?/|/g'`
# lopts_all='|aaa|bbb|ddd|eee|'
lopts_all=`echo "$lopts" | sed -e 's/://g'`
# lopts_arg='|ddd|eee|'
lopts_arg=`echo "$lopts" | sed -e 's/[^:|]\+|//g' -e 's/://g'`
while getopts "$sopts-:" OPTNAM; do
if [ "$OPTNAM" = '-' ]; then
if [ -n "`echo \"$OPTARG\" | grep '='`" ]; then
# --option=argument
OPTNAM=${OPTARG%=*}
OPTARG=${OPTARG#*=}
elif [ -n "`echo \"$OPTARG\" | grep -E \"^($lopts_arg)$\"`" ]; then
# --option argument
OPTNAM=$OPTARG
if [ $OPTIND -gt $# ]; then
echo "No arg for --$OPTNAM option" 1>&2
exit 1
fi
OPTARG=`eval echo \\$$OPTIND`
OPTIND=`expr $OPTIND + 1`
else
# --option
OPTNAM=$OPTARG
OPTARG=
fi
# CHECK
if [ -z "`echo \"$OPTNAM\" | grep -E \"^($lopts_all)$\"`" ]; then
echo "Illegal option --$OPTNAM" 1>&2
exit 1
fi
fi
case "$OPTNAM" in
a) opt_aaa;;
b|bbb) opt_bbb;;
ccc) opt_ccc;;
d) opt_ddd;;
e|eee) opt_eee;;
fff) opt_fff;;
v|version) print_version;;
h|help) print_help;;
*) exit 1;;
esac
done
shift `expr $OPTIND - 1`
# 実行結果の表示
test "$is_aaa" = 'True' && echo "is_aaa: $is_aaa"
test "$is_bbb" = 'True' && echo "is_bbb: $is_bbb"
test "$is_ccc" = 'True' && echo "is_ccc: $is_ccc"
test -n "$val_ddd" && echo "val_ddd: $val_ddd"
test -n "$val_eee" && echo "val_eee: $val_eee"
test -n "$val_fff" && echo "val_fff: $val_fff"
test -n "$*" && echo "rest_args: $*"
新しいオプションを追加する場合は、冒頭部分にオプションの設定、ヘルプメッセージのオプションの説明、"case"内の分岐を加えるだけで済みます。
Shell Scriptでロングオプションを解析する方法は、ネットにもいくつかあったのですが、実用的なものは見当たらなかったので、ご紹介しました。
たくさんの方に使っていただけますと幸いです。
前にもお話しましたが、初めてコンピューターを触ったのは、今から約30年前、大学にあったNeXTでした。それから、SunOS、Solaris、FreeBSD、Debian、Ubuntuと、一貫してUNIX系のOSを使い続けています。
UNIX系のOSでコンピューターを終了(再起動を含む。)する際には、管理者(root)権限でコマンドラインにshutdown、halt、reboot、poweroff(「shutdown等」といいます。)と入力します。
これらshutdown等は、入力すると「本当に終了しますか?」という意思確認をすることなく、コンピューターを終了してしまいます。そのため、間違って実行すると、作業中の内容が消えてしまったり、遠隔のサーバの電源が落ちてしまったりする危険性があります。
root> shutdown
(意思確認をすることなく、1分後にシャットダウン)
root> reboot
(意思確認をすることなく、すぐに再起動)
なお、この記事を書くにあたり、haltとrebootは別の意味で危険な可能性があることを知りましたが、その点はまた別の機会にお話したいと思います。
同じように危険なコマンドに、mkfsがあります。mkfsは、意思確認をすることなくストレージ(HDDやSSD)をフォーマットし、データを全部消してしまうので、非常に危険です。しかし、mkfsは少なくとも引数にデバイス名を指定する必要があり(mkfs.fatやmkfs.ext2などでないシンプルなmkfsは、オプションでファイルシステムの種類も指定する必要があります。)、コマンドのみで実行しても何もフォーマットできません。これに対して、shutdown等は、オプションや引数を指定する必要はなく、コマンドのみで実行してもコンピューターを終了できてしまいます。
root> mkfs (ここに少なくともデバイス名を指定する必要がある)
(エラーメッセージが表示されるだけ)
root> reboot (ここに何もいらない)
(すぐに再起動)
さらに、通常は、shutdown等にはデフォルトでパス(PATH)が通っていますので、フルパスを指定する必要はなく、コマンド名を入力するだけで実行できます。
root> reboot (/sbin/rebootと入力する必要はない)
(すぐにシャットダウン)
その上、管理者(root)のシェルが、昔は"Sh"だったので補完機能がなくコマンドをそのまま入力する必要がありましたが、今は"Bash"になってきていますので数文字入力するだけで補完できてしまいます。そのため、コマンド名全部を入力する必要はなく、数文字を入力して補完できてしまいます。もちろん、シェルをShに設定することもできますが、日本語名のファイルも普通にやり取りされている現代において、補完を使わずにすべて入力するのは、かなりの負担です。
root> reb (ここでTabを押す)
↓(補完される)
root> reboot
(すぐに再起動)
これらの結果、わずか数文字の入力で、コンピューターを終了できてしまいます。例えば、rebootは「r + e + b + Tab + Enter」というわずか5打鍵で実行でき、コンピューターを終了させることができてしまいます。
root> r + e + b + Tab + Enter (= reboot⏎)
(すぐに再起動)
これは非常に危険です。入力ミスで、コンピューターを終了してしまう可能性があります。例えば、rehashを実行するつもりで「r + e + h + Tab + Enter」と打鍵するはずが、うっかり"h"を"b"と打ち間違えた場合、rebootを実行してしまう可能性があります。なお、rehashはBashでは使わないので、そもそも入力する必要はありませんが、Zshではよく使うので、Zshユーザーは癖でうっかり入力してしまいそうです。そのような偶然はあまりないと思いますが、そもそも事故というものは偶然にミスが重なった場合に発生するものなので、あまりないからといって放っておいてよいものではありません。
なお、このような事故を防止するために、できる限り管理者(root)ではなく一般ユーザーで作業することが大切であることは、言うまでもありません。しかし、どうしても管理者(root)で作業しなければならないときもあります。
そこで、私は"/root/.bashrc"に次のような設定を加えています。
# /root/.bashrc
# shutdown、halt、reboot、poweroffを安全なaliasに設定
alias shutdown='printf %s "really? "; read a; test "$a" = "y" && shutdown'
alias halt=' printf %s "really? "; read a; test "$a" = "y" && halt'
alias reboot=' printf %s "really? "; read a; test "$a" = "y" && reboot'
alias poweroff='printf %s "really? "; read a; test "$a" = "y" && poweroff'
こうすると、意思確認をしてくれます。
root> reboot
really? (ここで「y」と回答)
(再起動)
ちなみに、"y"を"yes"や"Yes"に変えればもっと安全にすることができますが、そこまではしていません。
なお、どうしてもすぐにコンピューターを終了したい場合には、フルパスを指定するかyesを使うかすれば可能です。
root> /sbin/reboot
(すぐに再起動)
root> yes | reboot
(すぐに再起動)
たくさんの方に使っていただけますと幸いです。
パソコンは精密機器ですから、たまに故障します。
故障の原因で多いのは、ストレージ(HDDやSSD)の故障と電源ユニットの故障です。
ストレージは、小さなボディーの中で数千億ビットを超えるデータを保存する精密機器で、使用中は常に書込みや読込みという作業をしているため、物理的又は論理的に壊れやすいパーツです。しかし、使用する側も真っ先に疑うため、原因を特定しやすいといえます。特に、HDDの物理的な故障の場合は、異音がすることが多く、原因の特定が容易です。
これに対し、電源ユニットは、変電し給電するという単純作業をする部品で、ファンが回っている以外は状態に変化もないことから、使用する側に壊れるという認識が希薄です。しかも、壊れた場合に完全に電源が入らなくなってくれれば、原因を特定しやすいのですが、実際にはそうならない場合が多いです。そのため、電源ユニットを疑うのは最後になりがちです。
電源ユニットには、電力を安定させるために電解コンデンサーが使われています。この電解コンデンサーは時とともに劣化して、電力が安定しなくなります。電力が安定しなくなった結果、正常な動作を維持できなくなってフリーズしたり、ストレージに供給する電力が足りなくなってI/Oエラーになったりします。電解コンデンサーはマザーボードにも使われていますが、電源ユニットは高温で劣化が早く進むため、マザーボードよりも電源ユニットの方が壊れやすいのです。
この点に関して、既製品のパソコンを買い替えながら使っている場合と違い、自作パソコンの場合には特に注意が必要です。あっという間に時代遅れになってしまうCPU、その交換に伴って買い替える必要があるマザーボードとメモリは、定期的に買い替えざるを得ません(最近は、ブラウザ、メーラー、オフィスくらいしか使わないのであれば、かなり長期間、買い替えなくても、よくなりました)。その際、昔はCPUが新しくなるにつれて消費電力が増していましたので、電源ユニットも買い替える必要がありましたが、最近はCPUが省電力になってきており、電源ユニットを買い替える必要がなくなりました。その結果、電源ユニットは壊れるまで使い回される傾向にあり、気が付かないうちに劣化してしまっている可能性があるためです。
先日も、業務用のパソコンが突然フリーズし、やむなく再起動したところ今度はシャットダウンできなくなり、次に起動しようとした際にはI/Oエラー(入力・出力エラー)となって起動できなくなってしまいました。I/Oエラーなのでストレージやマザーボードの故障も疑ったのですが、過去の経験から電源ユニットの劣化を疑い、電源ユニットを交換したところ直りました。過去の経験がなければ、別のストレージにOSをインストールし直したり、マザーボード(ついでにCPUとメモリも)を買い替えたりしたかもしれません。
もしパソコンの調子が悪ければ、電源ユニットの故障を疑ってみてください。
サーバを操作する場合、"SSH"を使います。
SSHでサーバに接続していて、時間のかかるプログラムを実行させているうちにSSHが固まってしまった(フリーズしてしまった)、電話がかかってきて話をしているうちにSSHが固まってしまった(フリーズしてしまった)という経験をした方は多いと思います。原因は、一定時間、通信がなされないと、通信が切断されてしまうためだそうです(内部のネットワークからアクセスしているときは固まらないので、サーバではなく途中の通信機器が切断しているように思います。)。
これを回避するためには、クライアントPCの"/etc/ssh/ssh_config"又は"~/.ssh/config"というファイルに次のように書き込むと良いそうです。
# (ClientPC)/etc/ssh/ssh_config / (ClientPC)~/.ssh/config
# クライアントPCごとに設定しなければならず面倒
ServerAliveInterval 60
しかし、これらの方法は、クライアントPCごとに設定しなければならず、面倒です。サーバ側で設定できれば、1回の設定で終わるので便利です。
そこで、サーバ側の設定でなんとかならないかと考えますが、サーバの"/etc/ssh/sshd_config"というファイルに次のように書き込んでも、同じ効果が得られるそうです。
# (Server)/etc/ssh/sshd_config
# サーバの管理者(root)権限が必要で不便
ClientAliveInterval 60
しかし、この方法は、サーバの管理者(root)権限が必要で、不便です。
そこで、サーバ側の設定、しかも一般ユーザー権限の設定で、なんとかならないかと真面目に考えました。
答えは、"~/.bashrc"(理論的には"~/.profile"や"~/.bash_profile"が正しいのかもしれません。)というファイルに次の設定を書き込むことです(最後の&を忘れないように注意してください。)。
# (Server)~/.bashrc
# 一般ユーザーの権限で設定でき、しかも1回の設定で終わり簡単
test "$TERM" = 'dumb' || while ( sleep 60 ); do printf %b '\0'; done &
もちろん、この設定は、サーバにログインした際のシェルが"Bash"の場合です。"Sh"の場合は、"~/.shrc"に書き込む必要があります。Csh系のシェル("Csh"と"Tcsh")の場合には、"~/.cshrc"や"~/.tcshrc"に書き込む必要がありますが、"while"の文法が全く違うので、設定内容の文法を書き換える必要があります。
この設定では、最初に、環境変数"TERM"が"dumb"でないことを確認しています。これは、"SSHFS"(SSHを使ってサーバのディレクトリをクライアントPCにマウントするアプリ。)でないことを確認するためです。SSHFSでないことを確認できた場合、"while"と"sleep"を使って、60秒毎に"\0"をクライアントPCの端末に表示させています(実際には何も表示されません。)。"\0"をクライアントPCの端末に表示させる際に、サーバからクライアントPCに通信するため、通信が切断されないようになっています。表示させる文字は何でも良いのですが、アルファベットや記号などの普通の文字は、画面にそのまま表示されて操作の邪魔になります。エスケープ("\e")などの制御文字の多くは、誤動作の原因になりそうです。そこで、画面に表示されず、しかも誤動作の原因になりにくそうなヌル文字("\0")を表示させています。
この設定を入れてから、SSHが固まることはなくなりとても快適ですので、ぜひ使ってみてください。
それでも、通信状況が悪くて通信が途切れてしまい、SSHが固まってしまった場合は、"~."とタイプすると(チルダを押してピリオドを押す)、SSHから抜け出せます。
前回は"FreeWnn"の"Emacs"上での入力インターフェイスの"Tamago(egg)"の歴史と現状についてご説明し、最新のEmacsへの対応方法についてお話しました。実は、Tamago-tsunagi(Tamagoのバージョン5)を含むTamagoのバージョン4以降には重大な欠陥があります。
それは、辞書の編集機能がないことです。Tamagoのバージョン4以降でも、"egg-toroku-bunsetsu"(Ctrl-tで実行できます。)で新しい項目(単語)を登録することはできます。しかし、間違って登録した項目を削除することはできません。また、項目の頻度値(その項目をどの程度優先して使うかを定めた数値)を修正することもできません。Tamagoのバージョン3までは"edit-dict-item"というモードが附属していて、これを使って項目の削除や頻度値の修正ができました。しかし、Tamagoのバージョン4ではこのモードがなくなってしまいました。
確かに、辞書の編集機能は毎日使うようなものではありません。しかし、たまに間違って登録してしまい、項目を削除したい場合があります。また、正しい変換になるように、頻度値を修正したい場合もあります。このような場合、バイナリ形式の辞書をテキスト形式に変換して編集し、バイナリ形式に戻すという方法もあります。しかし、それはものすごい手間です。
そこでおすすめしたいのが、"XEmacs"の利用です。XEmacsはEmacsの派生の1つです。2009年ころから開発が止まっており、最新版でもバージョン21ですが(Emacsの最新版はバージョン27です。)、最新のLinux(Ubuntu20.04)でもサポートが継続しており、インストールが可能です。XEmacs21には、古いEmacs(Mule)の互換機能があり、Tamagoのバージョン3が動きます。このTamagoのバージョン3の"edit-dict-item"を使って、辞書の編集ができます。
XEmacsは標準でインストールされていないと思いますので、まずインストールする必要があります。Ubuntuであれば、管理者(root)権限で次のコマンドを実行します。なお、"root>"はコマンドプロンプトですので、入力する必要はありません。
root> apt-get install xemacs21-mule-canna-wnn
次に、XEmacsの設定ファイルを用意します。ホームディレクトリに.xemacsというディレクトリを作成し、次の内容でinit.elというファイルを作成します。
;;; ~/.xemacs/init.el
;;; FreeWnnの辞書編集に特化した設定
(setq wnn-jserver "localhost")
(set-language-environment "Japanese")
(setq default-input-method "japanese-egg-wnn")
(global-unset-key "\C-e")
(global-set-key "\C-e" 'edit-dict-item)
(toggle-input-method)
(ignore-errors (edit-dict-item "")) ; 1回目のエラー回避のため
Tamagoの設定ファイルはEmacsと共通で構いませんので、とくに準備する必要はありませんが、もしなければホームディレクトリに次の内容で.eggrcというファイルを用意します。
;;; ~/.eggrc
;;; 一般的なFreeWnnの辞書の設定
(defvar wnn-usr-dic-dir (concat "usr/" (user-login-name)))
(set-wnn-reverse nil)
(set-wnn-fuzokugo "pubdic/full.fzk")
(add-wnn-dict "pubdic/kihon.dic" (concat wnn-usr-dic-dir "/kihon.h") 10 nil t)
(add-wnn-dict "pubdic/special.dic" (concat wnn-usr-dic-dir "/special.h") 10 nil t)
(add-wnn-dict "pubdic/computer.dic" (concat wnn-usr-dic-dir "/computer.h") 5 nil t)
(add-wnn-dict "pubdic/bio.dic" (concat wnn-usr-dic-dir "/bio.h") 5 nil t)
(add-wnn-dict "pubdic/setsuji.dic" (concat wnn-usr-dic-dir "/setsuji.h") 0 nil t)
(add-wnn-dict "pubdic/symbol.dic" (concat wnn-usr-dic-dir "/symbol.h") -5 nil t)
(add-wnn-dict "pubdic/koyuu.dic" (concat wnn-usr-dic-dir "/koyuu.h") -5 nil t)
(add-wnn-dict "pubdic/jinmei.dic" (concat wnn-usr-dic-dir "/jinmei.h") -5 nil t)
(add-wnn-dict "pubdic/chimei.dic" (concat wnn-usr-dic-dir "/chimei.h") -5 nil t)
(add-wnn-dict "gerodic/g-jinmei.dic" (concat wnn-usr-dic-dir "/g-jinmei.h") -5 nil t)
(add-wnn-dict "pubdic/tankan.dic" "" -5 nil nil)
(add-wnn-dict "wnncons/tankan2.dic" "" -5 nil nil)
(add-wnn-dict (concat wnn-usr-dic-dir "/ud") nil 5 t t)
これで準備は終わりですが、私は操作方法を覚えられないので、次のような内容の読取り専用ファイルを~/.xemacs/manual.txtという名前で作り、これを起動時に開くようにしています。なお、xemacsは古いのでutf-8に対応していないため、このファイルの文字コードはeuc-jpにしておく必要があります。
edit-dict-item
C-e 辞書の編集を始めます。
n / C-n カーソルを下に移動します。
p / C-p カーソルを上に移動します。
a 辞書項目を追加します。
d カーソルの辞書項目を削除指定します。
u 削除指定された辞書項目の削除指定を解除します。
x 削除指定された辞書項目を実際に削除します。
M-h 辞書項目の頻度を設定します。
C-u 辞書項目の使用/不使用を切り替えます。
q 編集を終了します。
実際の起動は次のようにします。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> XMODIFIERS= xemacs21 ~/.xemacs/manual.txt
実際に起動して辞書編集中のものが、次の画像になります。
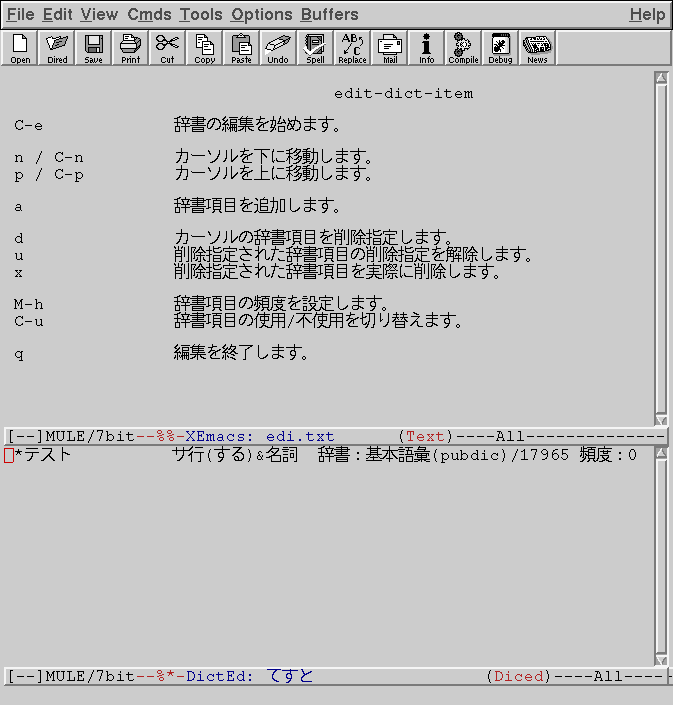
これで辞書編集が可能です。
Emacsのバージョン25以上で、Tamago-tsunagiを使って、FreeWnnで日本語入力できた話です。
前回もお話しましたが、漢字変換エンジン"FreeWnn"、エディタ"Emacs"、入力インターフェイス"Tamago(egg)"の組合せを、学生時代から今に至るまでずっと使っています。その間にいくつかの危機がありました。今回は、もっとも最近の危機についてお話したいと思います。
1997年にEmacsがバージョン20になった際、Tamagoのバージョン4が開発され、これが長らく使われてきました。
ところが、Emacsのバージョン24(正確には24.3のようです。)になると、Tamagoのバージョン4が動作しなくなってしまいました。そこで、さまざまなパッチが作られて使われていたようです。
2014年12月ころ、心ある有志の方がパッチを統合し、Tamago-tsunagi(Tamagoのバージョン5)という名前で公開してくださいました。これにより多くの方が救われました(心より敬意を表します。)。
ところが、Emacsのバージョン25になると、このTamago-tsunagiも正常に動作しなくなりました。
正常に動作しない点は、次の4点です。
1.の点については、漢字変換中にカーソル移動は頻繁に行う必要があり、1文字ずつ移動しなければならないのは非常に苦痛です。この点は致命的で、この点が改善されなければ、事実上、使いものになりません。
2.の点については、1.の点が解消すれば文節の先頭以外に移動しなくなるので、1.の点が改善されれば解決します。
3.の点については、もう一度、終了(Ctrl-x Ctrl-c)を実行すれば、今度はちゃんと終了します。終了は実行の頻度が小さいので負担は大きくありませんし、Emacsのバージョン26(ubuntu20.04)ではかなり改善しているようですので、なんとかなると思います。
4.の点については、その点に関する記事をネットで読んで、そのような機能があることを始めて知りました。多くの人は使っていない機能だと思いますし、よほど長い文章でなければ、入力し直せば良いので、なんとかなると思います。
そこで、1.の点の改善を試みました。
さっそく、カーソル移動のソースコードを探したところ、原因が"egg-cnv.el"にあることは分かったのですが、何が原因かはさっぱり分かりませんでした。
そこで、原因療法をあきらめて、対症療法で改善を試みました。1文字ずつしか移動しないのであれば、文節の頭まで1文字ずつ移動すれば良いということです。
修正したのは"egg-backward-bunsetsu"と"egg-forward-bunsetsu"の2つの関数です。最後に、3.の点の改善策を追加しました。
;;;======================================================;;;
;;; "egg-cnv.el"を修正
(defun egg-backward-bunsetsu (n)
(interactive "p")
(if (>= emacs-major-version 25)
(egg-backward-bunsetsu-current n)
(egg-backward-bunsetsu-v24-or-under n)))
(defun egg-backward-bunsetsu-current (n)
(interactive "p")
(while (and (> n 0)
(null (get-text-property (1- (point)) 'egg-start)))
(backward-char)
(while (equal (egg-get-bunsetsu-info (+ (point) 0))
(egg-get-bunsetsu-info (- (point) 1)))
(backward-char))
(setq n (1- n)))
(if (> n 0)
(signal 'beginning-of-buffer nil)))
(defun egg-backward-bunsetsu-v24-or-under (n)
(interactive "p")
(while (and (> n 0)
(null (get-text-property (1- (point)) 'egg-start)))
(backward-char)
(setq n (1- n)))
(if (> n 0)
(signal 'beginning-of-buffer nil)))
(defun egg-forward-bunsetsu (n)
(interactive "p")
(if (>= emacs-major-version 25)
(egg-forward-bunsetsu-current n)
(egg-forward-bunsetsu-v24-or-under n)))
(defun egg-forward-bunsetsu-current (n)
(interactive "p")
(egg-next-candidate 0) (egg-previous-candidate 0)
(while (and (>= n 0)
(null (get-text-property (point) 'egg-end)))
(while (equal (egg-get-bunsetsu-info (+ (point) 0))
(egg-get-bunsetsu-info (+ (point) 1)))
(forward-char))
(setq n (1- n)))
(if (null (get-text-property (1+ (point)) 'egg-end))
(forward-char)
(progn (while (equal (egg-get-bunsetsu-info (+ (point) 0))
(egg-get-bunsetsu-info (- (point) 1)))
(backward-char))
(signal 'end-of-buffer nil))))
(defun egg-forward-bunsetsu-v24-or-under (n)
(interactive "p")
(while (and (>= n 0)
(null (get-text-property (point) 'egg-end)))
(forward-char)
(setq n (1- n)))
(backward-char)
(if (>= n 0)
(signal 'end-of-buffer nil)))
;;;======================================================;;;
;;; "egg-com.el"を修正
;; エラーを無視して、強制的にEmacsを終了します。
;; 問題があれば、コメントアウトしてください。
(defun egg-kill-emacs-function () (ignore-errors (egg-finalize-backend)))
当初はTamago-tsunagiに当てるパッチとして公開することを考えましたが、単純な関数の修正なので、追加のファイルで公開することにしました。
"egg-tart.el"という名前で公開しますので、多くの方にダウンロードして使っていただければ幸いです。なお、文字コードはUTF-8です。ブラウザで開いた場合、設定によっては文字化けしますので、ご注意ください。
念のために使用法も書いておきます。
使用法
(1) このファイルは"tamago-tsunagi-5.0.7.1"を前提としていますので、
まず、"tamago-tsunagi-5.0.7.1"を"/usr"以下にインストールしてください。
(2) このファイルを"/usr/share/emacs/site-lisp/egg/"にコピーしてください。
(3) "~/.emacs"又は"~/.emacs.el"又は"~/.emacs.d/init.el"に、
;;;======================================================;;;
(add-to-list 'load-path "/usr/share/emacs/site-lisp/egg")
(require 'egg)
(load "/usr/share/emacs/site-lisp/egg/leim-list")
(load "/usr/share/emacs/site-lisp/egg/menudiag")
(load "/usr/share/emacs/site-lisp/egg/egg-tart")
(setq default-input-method "japanese-egg-wnn")
(setq wnn-jserver "127.0.0.1")
(setq egg-default-startup-file "~/.eggrc.el")
;;;======================================================;;;
などと書き込んでください。
なお、環境などに応じて、"127.0.0.1"を"localhost"に変えたり、
"~/.eggrc.el"を"~/.emacs.d/.eggrc.el"に変えたりしてください。
(4) "env XMODIFIERS= emacs"で"Emacs"を起動してください。
これでだいたい使えると思います。
なお、こんなものに著作権を主張するつもりは毛頭ないのですが、著作権を明示しておかないと後で困る人もいるかもしれないので、著作権を明示することにしました。それならばパブリックライセンスでも良かったのですが、そうすると複雑になるので、元のTamago-tsunagiのライセンスに合わせて"GNU General Public License(GPL)"のバージョン2又はその後のバージョン(GPL-2.0+)にしました。
毎日、仕事で日本語を入力しています。仕事でなくても、友人への連絡メールなどで日本語を入力しています。これらの入力の履歴は、たとえ個人の履歴であっても、ものすごい量です。そして、どのような単語をどのような頻度で使うのかを記録したビッグデータです。
日本語入力をしていると、しばしば変換できない単語に出会います。例えば「
また、日本語にはたくさんの同音異義語があり、すぐに思った単語に変換してくれないこともあります。例えば、「かし」という読みの単語には、「仮死」、「可視」、「歌詞」、「河岸」、「華氏」、「菓子」、「樫」、「貸し」、「瑕疵」、「下肢」などがあります。この中で一般の方が使うのは「歌詞」や「菓子」が多いと思います。しかし、法律関係の仕事で使うのは圧倒的に「瑕疵」(物や権利の欠点のこと)で、次に使うとすれば「下肢」(足のことで、「下肢の後遺障害」というように使います)です。刑事事件に力を入れていれば、取調べの録音・録画という意味の「可視化」で「可視」を使うかもしれません。このような変換の頻度の違いに応じて、変換候補を提案してくれなければ、スムーズに入力することはできません。最近の日本語入力システムはこのような変換の頻度の違いを記録しますが、このような記録を新しいパソコンに引き継ぐことはできません(できるのかもしれませんが、私は知りませんし、多くの方はやっていないと思います。)。
このように、日本語入力の履歴には大きな価値があります。これを有効に利用するためには、次の3つの機能が必要です。
1つ目は、変換辞書にない単語をその場で登録できる機能です。例えば、「がい+かん+ゆうち+ざい」で「外患誘致罪」と変換した場合や「がいこく+かんじゃ+ゆうち+はんざい」から「外患誘致罪」を作った場合に、その場で単語登録できる機能です。もちろん専用の単語登録アプリでも同じことができますが、文書の作成中にいちいち専用の単語登録アプリを起動する気にはなりません。
2つ目は、同音異義語の変換頻度を自動的に記録し、必要に応じて調整できる機能です。例えば、「かし」で「瑕疵」と変換することが多ければその頻度を記録し、それが行き過ぎて「おかし」で「お菓子」ではなく「お瑕疵」と変換するようになった場合には調整できる機能です。
3つ目は、そのような記録をパソコンからデータとして取り出し、他のパソコンから取り出したデータと比較したり、新しいパソコンに引き継いだりできる機能です。
これら3つの機能を実現する方法として、漢字変換エンジン"FreeWnn"、エディタ"Emacs"、入力インターフェイス"Tamago(egg)"の組合せを、学生時代から今に至るまでずっと使っています。登録した単語は地名なども含めて10万語を優に超えています。今まで幾度となく新しい日本語入力システムに移行しようとしましたが、最終的にこれら3つの機能がネックになり、移行できませんでした。いつか、この組合せを超える日本語入力システムがあれば移行を考えたいと思いますが、当分の間は無理そうです。
データを保存したり他人に渡したりするとき、CD-RやDVD-Rのディスクにデータを焼くことがあります。
その際、データがディスクの最大容量に収まっているかどうかが分からず、苦労することがあります。
そこで、ディスクの最大容量を調査しましたので、備忘を兼ねて公開します。
CD-Rは、736,931,840byteのISOイメージまで焼けました。中身のファイルは736,561,152byteまで焼けました。
1層のDVD-Rは、4,706,074,624byteのISOイメージまで焼けました。中身のファイルは、ファイルシステム(ISO 9660)の仕様で、原則として4MiBまでしか焼けません(実際には2byte少ない4,294,967,294byteまでしか焼けませんでした。)。
CD-Rには通常「700MB」と書かれていますが、これは「700MiB」のようです(1Mib=1024×1024byte=1,048,576byte)。
これに対して、1層のDVD-Rには通常「4.7GB」と書かれていますが、これはそのまま「4.7GB」のようです(1GB=1000*1000*1000byte=1000,000,000byte)。
同じような表記でも単位が違うので、注意が必要ですね。
まとめると、CD-Rは736,931,840byteまで、1層のDVD-Rは4,706,074,624byteまでです(メディアや環境によって多少の違いがあるかもしれません。)。
前回はMigemoがとても便利な話をしました。Migemoは日本語をローマ字で検索するソフトウェアです。「kodomo」と入力するだけで、「子供」を検索できます。
Migemoは訓令式やヘボン式のローマ字規則に対応していますので、普通のキーボードを使っているのであれば、ローマ字規則を変える必要はないと思います。
しかし、世の中には普通ではないキーボードを使っている人がいます。例えばDvorak配列のキーボードです。Dvorak配列については、後日、またお話したいと思います。Dvorak配列は非常に優れた配列ですが、"k"や"y"の位置が少し不便なため、ローマ字入力の際、か行の入力に"k"の代わりに"c"を、拗音の入力に"y"の代わりに"h"や"n"を使うアイディアが考案されました(このアイディアはDvorakJPの一部です。DvorakJPは非常に優れたアイデアです。心より敬意を表します。)。
ローマ字入力に、DvorakJPのような変則的なローマ字規則を使う場合、当然、Migemoのローマ字規則も変更したくなります。その設定方法をご紹介します。設定方法は、Rubyで書かれた伝統的なmigemoとC言語で書かれた新しいcmigemoで違います。
伝統的なmigemoでは、"/usr/lib/ruby/1.8/romkan.rb"を編集します。具体的には次のような行を書き加えます。
# /usr/lib/ruby/1.8/romkan.rb
か ca き ci く cu け ce こ co
っか cca っき cci っく ccu っけ cce っこ cco
きゃ cna きゅ cnu きょ cno
っきゃ ccna っきゅ ccnu っきょ ccno
ちゃ tna ちゅ tnu ちょ tno
っちゃ ttna っちゅ ttnu っちょ ttno
にゃ nha にゅ nhu にょ nho
っにゃ nnha っにゅ nnhu っにょ nnho
ひゃ hna ひゅ hnu ひょ hno
っひゃ hhna っひゅ hhnu っひょ hhno
みゃ mna みゅ mnu みょ mno
っみゃ mmna っみゅ mmnu っみょ mmno
りゃ rha りゅ rhu りょ rho
っりゃ rrha っりゅ rrhu っりょ rrho
ぎゃ gna ぎゅ gnu ぎょ gno
っぎゃ ggna っぎゅ ggnu っぎょ ggno
じゃ zha じゅ zhu じょ zho
っじゃ zzha っじゅ zzhu っじょ zzho
ぴゃ pna ぴゅ pnu ぴょ pno
っぴゃ ppna っぴゅ ppnu っぴょ ppno
びゃ bna びゅ bnu びょ bno
っびゃ bbna っびゅ bbnu っびょ bbno
新しいmigemoでは、"/usr/share/cmigemo/utf-8/roma2hira.dat"(ubuntu等の場合)又は"/usr/share/migemo/utf-8/roma2hira.dat"(mac等の場合)を編集します。具体的には次のような行を書き加えます。
# /usr/share/cmigemo/utf-8/roma2hira.dat / /usr/share/migemo/utf-8/roma2hira.dat
ca か
ci き
cu く
ce け
co こ
cna きゃ
cnu きゅ
cno きょ
tna ちゃ
tnu ちゅ
tno ちょ
nha にゃ
nhu にゅ
nho にょ
hna ひゃ
hnu ひゅ
hno ひょ
mna みゃ
mnu みゅ
mno みょ
rha りゃ
rhu りゅ
rho りょ
gna ぎゃ
gnu ぎゅ
gno ぎょ
zha じゃ
zhu じゅ
zho じょ
dna ぢゃ
dnu ぢゅ
dno ぢょ
bna びゃ
bnu びゅ
bno びょ
pna ぴゃ
pnu ぴゅ
pno ぴょ
これにより、「codomo」で「子供」が、「toucno」で「東京」が検索できるようになります。
私はMigemoをとても愛用しています。Migemoは日本語をローマ字で検索するソフトウェアです。
例えば文章データの中から「子供」を検索したい場合、通常の検索であれば、検索窓を開いて「kodomo」と入力し、スペースキーを数回押して「子供」と漢字変換しなければ、「子供」を検索できません。
これに対して、Migemoを使った検索であれば、「kodomo」と入力するだけで、「子供」を検索できます。漢字変換しなくても良いのです。
たったそれだけかと思われるかも知れませんが、「交渉」、「高尚」、「公称」、「工廠」のように同音異義語が多い言葉の場合に非常に助かります。
また、Migemoを使えば、「kodomo」と入力するだけで、「子供」だけでなく「子ども」や「こども」も検索できます。表記の揺れを気にしなくて良いのです。
特に「kodomo」の場合、伝統的な表記は「子供」ですが、お供を連想させるということで「子ども」にすべきだという意見がある一方で、5月5日の祝日は「こどもの日」となっており、表記が揺れが大きく、非常に助かります。
残念ながらデメリットもあります。予想外のものがヒットすることです。「kodomo」で検索すると、入場料や乗車賃の区分を表す「小人」もヒットしてしまいます。音だけで検索しますので、全く別の意味の言葉もヒットしてしまうのです。
もっとも、1つの文章の中に音が同じ言葉が多量に含まれていることはあまりなく、仮に別の意味の言葉がヒットしても飛ばして次の候補に進めば良いので、それほど気になりません。どうしても気になる場合には、Migemoを一時停止して、通常の検索をするという手段もあります。
このように非常に便利なMigemoですが、使うことができるソフトウェアは限られています。私が知る限りでは、エディタのEmacs、テキストブラウザのW3mの2つだけです。今回この記事を書くに際し、ネットで検索して見たところ、エディタのVimなど、他にもなくはないようですが、いずれにしても非常に限られています。それらに、私が作成し公開している"sazae(栄螺)"(コマンドラインシェルZsh上で、コマンドを入力する際に、Migemoを使って日本語のファイル名を補完します。)を含めても片手で数えるほどしかありません。
かつて、ブラウザのFirefoxで、Migemoのアドオンがあり、Migemoを使ってページ内を検索できた時期がありましたが、すぐにバージョンが合わなくなり使えなくなってしまいました。
個人的には、FirefoxやChromeなどのブラウザで使えると、便利だと思うので、どなたか開発していただけないかと思っていますし、そう思っているのは私だけではないと思います(「じゃあ、お前が作れ!」と言われそうですが…)。
Migemoの作者に敬意を表するとともに、Migemoが広く社会に普及することを願い、本記事を公開いたします。
なお、Migemoは変わった名前ですが、友人と雑談をしているときの「にゃんマゲみたいにポケモンにマゲをつけてマゲモンはどうだろうか」という発言が発端となり、googleの検索結果も考慮して、「マゲモン → マゲモ → Magemo → Migemo」となったそうです。
今回は非常にお恥ずかしいお話をします。
初めてコンピューターを触ったのは、今から約30年前、大学にあったNeXTでした。NeXTは、スティーブ・ジョブズが作ったUNIX系のワークステーションです。ちなみに、その時、何をどうしてよいのかが全く分からなかった私は、とりあえずデスクトップ上のアイコンをクリックしてみたのですが、そのままコンピューターがフリーズしてしまい、相談した管理者の方に「これは立ち上げたらダメって言っているでしょ!」と怒られ、私のコンピューター初体験はわずか30秒で終わってしまいました。それから現在に至るまで、仕事も含めて一貫して、UNIX系のOS(FreeBSD、Linuxなど)を使い続けています。
UNIXでは、OSの設定も含めて、あらゆる場面でテキストファイルを使います。テキストファイルとは、Windows上では拡張子".txt"で表されるファイルで、簡単いうと文字と記号のみで記載されたファイルです。なぜテキストファイルかというと、テキストファイルであれば、特殊なソフトを必要とせずにファイルの閲覧や編集ができますし、バックアップを取ったりファイルの内容を比較したりすることも簡単だからです。この辺りのお話は、ぜひ名著「UNIXという考え方 - その設計思想と哲学」をお読みください。
さて、テキストファイルであれば、ファイルの内容を比較したりすることも簡単ということですが、ファイルの内容の比較は非常に頻繁に行ないます。例えば、このページのようにファイルを編集し続けてきた場合、今日の時点のファイルと先月の時点のファイルを比較して、どこが変わったのかを確認したりするような場合です。
ファイルの内容を比較するコマンドが"diff"です。diffは次のようにして使います。なお、"sh>"はコマンドプロンプトですので、入力する必要はありません。
sh> diff a.txt b.txt
2d1
< Store numerical data in flat ASCII files.
この結果は、どちらかのファイルが1行だけ多く、その行が「Store numerical data in flat ASCII files.」であるということを意味しています(ちなみに、「Store numerical data in flat ASCII files.」は「UNIXという考え方 - その設計思想と哲学」に出てくるUNIXの思想の1つで、テキストファイルを使うべきだという意味です。)。出力の行頭の"<"はどちらのファイルなのかを示す記号です。もう一方のファイルを示す場合には行頭の">"が使われます。ここまでは、私にもすぐに分かりました。問題は"<"が"a.txt"と"b.txt"のどちらを意味するかです。
お間抜けな私は、何度diffを実行しても"<"と">"がどちらのファイルを意味しているのかを覚えられず、約30年の長期に渡り、diffを実行したあと、わざわざファイルの中身を見て、どちらのファイルであるかを確認していました。あまりにめんどくさいので、"<"と">"の代わりに、"A"と"B"に変えて、コンパイルしてやろうかと思っていたほどでした。
それが、先日、ふと気が付きました。"<"と">"は"←"と"→"という意味であり、左側の引数と右側の引数を示しているということに…。したがって、先の例であれば、"<"は左側の引数である"a.txt"を意味しています。
約30年の間に、おそらく数千回もdiffを実行してきたはずなのに、全く気が付きませんでした。
私と同じように気が付いていない方がおられたらと思い、恥を忍んで記事にいたしました。
5年ほど前に真っ白なキーボードに憧れて、キートップ(キーの上面)に文字の刻印のない無刻印キーボードを購入し、使いはじめました。
どうせタッチタイピングするのでキートップなんて見ないし、そもそもキー配列を独自配列に変更するので(どのように変更しているのかは"akauni(赤海胆)"をご参照ください。)、キートップは真っ白で構わない、むしろ文字の刻印なんて無駄だと思っていたのです。
無刻印キーボードはとても快適でした。そのシンプルな見た目にほれぼれしながら使っていました。パスワードを設定するときを除いては。そう、パスワードを設定するときを除いては。
私は、キーボードで入力する際、常にタッチタイピングしていると思っていました。しかし、パスワードを設定するときだけは、キートップの文字の刻印を見ながら入力していたのです。
ところで、私たちがキーボードを使って文字を入力する際、一定の割合で入力ミスをしています。通常は、すぐに入力内容が画面に表示されるため(入力内容が画面に表示されることを、エコーバックと呼びます。)、すぐに入力ミスに気が付いて訂正しています。
ところが、パスワード入力の際には、エコーバックがありません。あったとしても"*"などの記号が表示されるだけです。そのため、入力ミスに気が付かない可能性があります。入力ミスに気が付かなかったとしても、パスワードを解除する際であれば、再入力すれば良いので、この場合は問題はありません。また、ネットの会員ページなどにアカウントを作る際であれば、メールを利用して新しいパスワードを再設定することが可能ですので、この場合も問題はありません。
問題は、ファイルにパスワードを設定して暗号化する場合です。パスワードの設定で入力ミスをした場合、ファイルを復号できなくなってしまう可能性があります。パスワードの再設定も不可能ですので、二度とファイルを複合できなくなり、事実上、データは失われてしまいます。ファイルにパスワードを設定して暗号化する場合は、このような危険が伴うため、慎重に入力すべきなのです。
5年ほど無刻印キーボードを使い、キーの感覚は指が覚えていますが、それでもパスワードの設定は恐くてできません。
無刻印キーボードはこの欠点を踏まえても余りある魅力があると思いますが、もし新たに購入しようと考えている方がおられましたら、注意が必要だと思います。
前回は斜めから撮影した写真を真っ直ぐに補正する話をしました。その際、横の幅について、画像の左から右に行くに従って、文字の幅が狭くなっていたことから、これを補正する関数として次の関数を導入しました。
# 幅のゆがみを直す手動補正
def correct_width(out_z, siz_z, par_z):
add_z = par_z * math.sin(math.pi * out_z / siz_z) # 三角関数
# add_z = par_z * out_z * (siz_z - out_z) / (siz_z * siz_z / 4) # 2次関数
in_z = out_z + add_z
return in_z
少し説明を補足しておきます。
この関数は"for"ループの中で出力画像の座標から入力画像の座標を求める際、出力画像の座標を修正する関数です。出力画像の座標をあらかじめ修正し、修正した出力画像の座標から入力画像の座標を求めることにより、幅を補正しています。
出力画像の座標から入力画像の座標を求め、求めた入力画像の座標を修正する方法も考えられますが、入力画像の補正すべき領域は長方形ではないため、下手に修正すると補正すべき領域からはみ出してしまいますので、出力画像の座標を修正する方が入力画像の座標を修正するよりも簡単です。
出力画像の座標を修正する関数については、次の2点を満たす必要があります。
1.の条件は、入力画像の補正すべき領域がきれいに出力画像に収まるために必要な条件です。出力画像の座標の両端で関数の値が0でないと、入力画像の補正すべき領域の境界にならないため、補正すべき領域が出力画像に入っていなかったり、補正すべき領域の外が出力画像に入ってしまったりしてしまうので、不都合です。
2.の条件は、出力画像に滑らかであるために必要な条件です。関数の傾きが増加や減少を繰り返すと、出力画像の座標の修正の幅が広くなったり狭くなったりして、出力画像が波打ってしまいますので、不都合です。
これらの条件を満たす関数として、すぐに思い付くのが、三角関数の山の部分です。
add_z = par_z * math.sin(math.pi * out_z / siz_z) # 三角関数
出力画像の右端、すなわち"out_z"が"0"で0になるように正弦関数を選択し、出力画像の左端、すなわち"out_z"が"siz_z"で0になるように、"out_z"に"π / siz_z"を掛けています。"par_z"を掛けて補正の程度を指定しています。
次に思い付くのが、2次関数です。
add_z = par_z * out_z * (siz_z - out_z) / (siz_z * siz_z / 4) # 2次関数
出力画像の両端、すなわち、out_zが0又はsiz_zで関数の値がゼロになるように"out_z"と"siz_z - out_z"を掛け合わせています。頂点の高さが1になるように"(siz_z * siz_z / 4)"で割ったうえで、"par_z"を掛けて補正の程度を指定しています。
実際に補正の様子を試してみます。
用意したのは次の画像です。単純なしま模様です。

三角関数を使った補正のプログラムは次のコードです。分かりやすいように、補正の程度を大きめの64にしてあります。なお、補正の大きさを大きくし過ぎると、導関数が-1を下回ってしまいます。そうすると、出力画像が右に移動したにもかかわらず、対応する入力画像のピクセルが左に移動するようなことになってしまいますので注意が必要です。
#!/usr/bin/python3
# quadratic.py
# 三角関数を使った補正
from PIL import Image
IN_FILE = 'barcode.png'
OUT_FILE = 'quadratic.png'
def correct_width(out_z, siz_z, par_z):
add_z = par_z * math.sin(math.pi * out_z / siz_z) # 三角関数
#add_z = par_z * out_z * (siz_z - out_z) / (siz_z * siz_z / 4) # 2次関数
in_z = out_z + add_z
return in_z
in_img = Image.open(IN_FILE).convert('RGB')
out_img = Image.new('RGB', (in_img.size[0], in_img.size[1]))
siz_x = in_img.size[0] - 1
for out_x in range(in_img.size[0]):
in_x = correct_width(out_x, siz_x, 64)
c = in_img.getpixel((in_x, 0))
for y in range(in_img.size[1]):
out_img.putpixel((out_x, y), c)
out_img.save(OUT_FILE)
結果は次の画像です。

2次関数を使った補正のプログラムは次のコードです。同じように、補正の大きさを大きめの64にしてあります。なお、補正の大きさを大きくし過ぎると、問題が生じるのは三角関数の場合と同じです。
#!/usr/bin/python3
# quadratic.py
# 2次関数を使った補正
from PIL import Image
IN_FILE = 'barcode.png'
OUT_FILE = 'quadratic.png'
def correct_width(out_z, siz_z, par_z):
#add_z = par_z * math.sin(math.pi * out_z / siz_z) # 三角関数
add_z = par_z * out_z * (siz_z - out_z) / (siz_z * siz_z / 4) # 2次関数
in_z = out_z + add_z
return in_z
in_img = Image.open(IN_FILE).convert('RGB')
out_img = Image.new('RGB', (in_img.size[0], in_img.size[1]))
siz_x = in_img.size[0] - 1
for out_x in range(in_img.size[0]):
in_x = correct_width(out_x, siz_x, 64)
c = in_img.getpixel((in_x, 0))
for y in range(in_img.size[1]):
out_img.putpixel((out_x, y), c)
out_img.save(OUT_FILE)
結果は次の画像です。

二つを上下に並べてみました。上が三角関数、下が2次関数です。

2次関数の方が補正の程度が若干強いようです。
書面等の写真を撮影する際、真っ直ぐ上から撮影しようとすると、自分の影ができてしまうため、斜めから撮影せざるを得ない場合があります。また、完全に真っ直ぐ上から撮影することはかなり難しく、真っ直ぐ上から撮影したつもりでも、多くの場合は斜めから撮影しています。
このように斜めから撮影した場合であっても、読むだけであれば、多くの場合は問題ではありません。しかし、文字認識(OCR)にかける場合などには、写真を真っ直ぐに補正する必要があります。
今回は、斜めから撮影した写真を真っ直ぐに補正することを考えてみます。
斜めから写真を撮影すると、正方形が歪み、普通の四角形になります。一般的に平行四辺形や台形にもなりません。
下の図は、これをイメージしたものです。左の四角形OXZYを写真に撮影したところ、右の四角形ABDCになったとします。
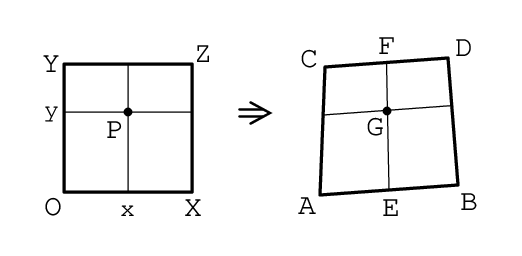
今後の計算のために、"X"で線分OXの長さを、"x"で線分Oxの長さを、"Y"で線分OYの長さを、"y"で線分Oyの長さを表すことにします。
また、右の四角形について、適切な点を原点に取り、"A"で原点を始点とし終点を点Aとするベクトルを、"B"で原点を始点とし終点を点Bとするベクトルを、"C"で原点を始点とし終点を点Cとするベクトルを、"D"で原点を始点とし終点を点Dとするベクトルを、"E"で原点を始点とし終点を点Eとするベクトルを、"F"で原点を始点とし終点を点Fとするベクトルを、"G"で原点を始点とし終点を点Gとするベクトルを表すことにします。
左の四角形の点Pに対応する点を、右の四角形の点Gとします。
そうすると、線分AEの長さと線分EBの長さの比率は、線分Oxの長さと線分xXの長さの比率は等しくなります。また、線分CFの長さと線分FDの長さの比率も、線分Oxの長さと線分xXの長さの比率は等しくなります。さらに、線分EGの長さと線分GEの長さの比率は、線分Oyの長さと線分yYの長さの比率は等しくなります。
これをベクトルを使って表すと、次のようになります。
E = {(X-x)/X}A + (x/X)B = {(X-x)A + xB} / X
F = {(X-x)/X}C + (x/X)D = {(X-x)C + xD} / X
G = {(Y-y)/Y}E + (y/Y)F = {(Y-y)E + yF} / Y
ベクトルGの式に、ベクトルEとベクトルFを代入して整理します。
G = [{(X-x)A + xB} / X] (Y-y)/Y + [{(X-x)C + xD} / X] y/Y
= {(X-x)(Y-y)A + x(Y-y)B + (X-x)yC + xyD} / XY
これが、点Gの座標になります。点A、B、C、Dの重み付き平均になっています。
なお、今は、四角形OXZYの点Pの座標から四角形ABDCの点Gの座標を求めましたが、逆に、四角形ABDCの点Gの座標から四角形OXZYの点Pの座標を求めるという方法も考えられます。しかも、その方が自然な考え方かもしれません。しかし、この考え方はうまくいきません。なぜならば、四角形OXZYの点の数が四角形ABDCの点の数よりも多い場合などに、四角形OXZYの点に色が決まらない点が出てくるからです。
実際の写真で補正してみます。
使用するのは、次の写真です。看板部分を真っ直ぐに補正してみます。なお、後ろの建物は検察庁の建物ですが、念のためにぼやかせました。

看板部分だけを拡大すると、次の写真になります。

上記のアルゴリズムをPythonで実装したのが、次のコードになります。
#!/usr/bin/python3
# correctid-simple.sy
# 看板部分を真っ直ぐに補正するプログラム
from PIL import Image
# 入力ファイル名を指定します
IN_FILE = 'in_image.jpg' # 看板の拡大写真
# 事前に調べておいた看板の四つ角を指定します
COR_TL = (119, 54) # 上左
COR_TR = (505, 578) # 上右
COR_BL = ( 40, 581) # 下左
COR_BR = (476, 1036) # 下右
# 出力ファイル名を指定します
OUT_FILE = 'out_image-simple.jpg'
# 出力画像のサイズを指定します
OUT_SIZE_X = 600
OUT_SIZE_Y = 300
# 入力画像をRGBで読み込みます
in_img = Image.open(IN_FILE).convert('RGB')
# 入力画像を配列にしておきます
in_arr = []
for x in range(in_img.size[0]):
arr = []
for y in range(in_img.size[1]):
arr.append(in_img.getpixel((x, y)))
in_arr.append(arr)
# 出力画像のフォーマットを作成します
out_img = Image.new('RGB', (OUT_SIZE_X, OUT_SIZE_Y))
# 出力画像を作成します
siz_x = OUT_SIZE_X - 1
siz_y = OUT_SIZE_Y - 1
for out_x in range(OUT_SIZE_X):
tmp_x = out_x
pmt_x = siz_x - tmp_x
for out_y in range(OUT_SIZE_Y):
tmp_y = out_y
pmt_y = siz_y - tmp_y
# 出力画像の座標から入力画像の座標を求めます
in_x = ((COR_TL[0] * pmt_x * pmt_y) +
(COR_TR[0] * tmp_x * pmt_y) +
(COR_BL[0] * pmt_x * tmp_y) +
(COR_BR[0] * tmp_x * tmp_y)) / siz_x / siz_y
in_y = ((COR_TL[1] * pmt_x * pmt_y) +
(COR_TR[1] * tmp_x * pmt_y) +
(COR_BL[1] * pmt_x * tmp_y) +
(COR_BR[1] * tmp_x * tmp_y)) / siz_x / siz_y
# 出力画像の色を求めます(最近傍補間法(ニアレストネイバー法))
out_rgb = [0, 0, 0]
in_x_int = round(in_x)
in_y_int = round(in_y)
for i in range(3):
out_rgb[i] = in_arr[in_x_int][in_y_int][i]
# 色の書き込み
out_img.putpixel((out_x, out_y), (out_rgb[0], out_rgb[1], out_rgb[2]))
# 保存
out_img.save(OUT_FILE)
少し説明しておきます。
入力ファイルに"in_image.jpg"を、出力ファイルに"out_image-simple.jpg"を指定しています。
看板部分の範囲を特定するため、事前にGIMPで看板部分の四つ角を調べて指定しておきました。
点A、B、C、Dの座標として、"COR_BL"、"COR_BR"、"COR_TL"、"COR_TR"を使っています。
なお、一般的に、Y軸は上に行くほど値が大きくなるように定義しますが、画像処理においては、Y軸は下に行くほど値が大きくなるように定義されることが多く、Pythonでもそのように定義されています。
最後の"for"ループの中で出力画像の座標から入力画像の座標を求めています。計算上、入力画像の座標は小数になりますので、小数部分を四捨五入して整数値にし、入力画像の色を参照しています。
実行すると、次の画像が出来上がります。

これで目的は達したのですが、ちょっと気になる点がいくつかあります。
まず、全体的に色が薄暗く、文字を読みにくいです。
また、画質について、全体的にざらついているように思います。これは、最近傍補間法(ニアレストネイバー法)の考え方により、入力画像の座標の小数部分を四捨五入して、単純に求められた座標の色を参照しているためだと思われます。
さらに、横の幅について、画像の左から右に行くに従って、文字の幅が狭くなっています。「広島合同庁舎」の「広」の文字と「舎」の文字では、だいぶ幅が違います。縦の幅についても、下の「広島合同庁舎」に比べて、上の「裁判所」は、わずかですが縦の幅に短いように思います。
これらを修正したものが、次のコードになります。
#!/usr/bin/python3
# correctid.py
# 看板部分を真っ直ぐに補正するプログラムの改良版
from PIL import Image
import math
# 入力ファイル名を指定します
IN_FILE = 'in_image.jpg' # 看板の拡大写真
# 事前に調べておいた看板の四つ角を指定します
COR_TL = (119, 54) # 上左
COR_TR = (505, 578) # 上右
COR_BL = ( 40, 581) # 下左
COR_BR = (476, 1036) # 下右
# 出力ファイル名を指定します
OUT_FILE = 'out_image.jpg'
# 出力画像のサイズを指定します
OUT_SIZE_X = 600
OUT_SIZE_Y = 300
# 入力画像をRGBで読み込みます
in_img = Image.open(IN_FILE).convert('RGB')
# 入力画像を配列にしておきます
in_arr = []
for x in range(in_img.size[0]):
arr = []
for y in range(in_img.size[1]):
arr.append(in_img.getpixel((x, y)))
in_arr.append(arr)
# 出力画像のフォーマットを作成します
out_img = Image.new('RGB', (OUT_SIZE_X, OUT_SIZE_Y))
# 幅のゆがみを直す手動補正
def correct_width(out_z, siz_z, par_z):
add_z = par_z * math.sin(math.pi * out_z / siz_z) # 三角関数
# add_z = par_z * out_z * (siz_z - out_z) / (siz_z * siz_z / 4) # 2次関数
in_z = out_z + add_z
return in_z
# 線形補間法(バイリニア法)
def bilinear(in_x, in_y, in_arr):
out_rgb = [0, 0, 0]
in_x_int = int(in_x)
in_x_dec = in_x - in_x_int
in_x_ced = 1 - in_x_dec
in_y_int = int(in_y)
in_y_dec = in_y - in_y_int
in_y_ced = 1 - in_y_dec
for i in range(3):
zz = in_arr[in_x_int + 0][in_y_int + 0][i] * in_x_ced * in_y_ced
pz = in_arr[in_x_int + 1][in_y_int + 0][i] * in_x_dec * in_y_ced
zp = in_arr[in_x_int + 0][in_y_int + 1][i] * in_x_ced * in_y_dec
pp = in_arr[in_x_int + 1][in_y_int + 1][i] * in_x_dec * in_y_dec
out_rgb[i] = round(zz + pz + zp + pp)
return out_rgb
# 色を明るくする手動補正
def correct_color(old_rgb):
new_rgb = [0, 0, 0]
for i in range(3):
new_rgb[i] = old_rgb[i] * 3
if(new_rgb[i] > 255):
new_rgb[i] = 255
return new_rgb
# 出力画像を作成します
siz_x = OUT_SIZE_X - 1
siz_y = OUT_SIZE_Y - 1
for out_x in range(OUT_SIZE_X):
tmp_x = correct_width(out_x, siz_x, 40) # 左を狭め右を広げる補正
pmt_x = siz_x - tmp_x
for out_y in range(OUT_SIZE_Y):
tmp_y = correct_width(out_y, siz_y, -5) # 上を広げ下を狭める補正
pmt_y = siz_y - tmp_y
# 出力画像の座標から入力画像の座標を求めます
in_x = ((COR_TL[0] * pmt_x * pmt_y) +
(COR_TR[0] * tmp_x * pmt_y) +
(COR_BL[0] * pmt_x * tmp_y) +
(COR_BR[0] * tmp_x * tmp_y)) / siz_x / siz_y
in_y = ((COR_TL[1] * pmt_x * pmt_y) +
(COR_TR[1] * tmp_x * pmt_y) +
(COR_BL[1] * pmt_x * tmp_y) +
(COR_BR[1] * tmp_x * tmp_y)) / siz_x / siz_y
# 出力画像の色を求めます(線形補間法(バイリニア法))
out_rgb = bilinear(in_x, in_y, in_arr) # 線形補間法
out_rgb = correct_color(out_rgb) # 色を明るくする補正
# 色の書き込み
out_img.putpixel((out_x, out_y), (out_rgb[0], out_rgb[1], out_rgb[2]))
# 保存
out_img.save(OUT_FILE)
まず、全体的に明るくするため、シンプルに各点の明るさを3倍にしました。もう少し複雑なアルゴリズムを採用すれば、実物の雰囲気が増すとは思いましたが、今回は本質的な問題ではないので止めました。
また、画質について、ざらつきをなくすため、線形補間法(バイリニア法)の考え方を採用し、入力画像の座標に近い4点の重み付き平均を取りました。式を見ていただければ分かりますが、出力画像の座標から入力画像の座標を求めるアルゴリズムは、線形補間法(バイリニア法)のアルゴリズムと全く同じです。すなわち、入力画像の座標を求めるのに、重み付き平均を取り、求まった座標から出力画像の色を求めるのに、また重み付き平均を取っているのです。
さらに、縦と横の幅について、出力画像の座標から入力画像の座標を求める計算式に、通常の線形関数に加え、三角関数を付加して、補正しました。この補正については、私の思付きで導入したものです。角度による見え方の問題なので、三角関数を使いましたが、論理的な裏付けがあるわけではありません。参考に、2次関数を使ったものをコメントアウトで残しておきました。ただし、こちらを使う場合にはパラメーターを調整し直す必要があります。もしかしたら、もっと合理的なアルゴリズムがあるかもしれません。
実行すると、次の画像が出来上がります。

注目すべきは、全体的に文字の下地は薄い水色になっていますが、「裁判所」の「所」の文字の左部分は白くなっています。元の画像で確認したところ、検察庁の建物が鏡のように写り込んでいて、白っぽくなっているのが、残っているようです。
なお、今回は、実物の雰囲気の残したかったので、あえて二値化(白黒などの二色にすること)しませんでしたが、二値化すればもっと見やすくなると思います。
元々が長方形の看板なので、補正すればきれいな長方形になるのは当たり前なのですが、きれいな長方形になったのを見ると、ちょっと感動します。
複数の動画を一気に編集しようとして、FFmpegをShell Scriptで使ったら予想外の結果になり、はまった話です。
次のようなShell Scriptを作成し、"a.mp4"、"b.mp4"及び"c.mp4"を用意して、実行します。
#!/bin/sh
# 正常に動作しない
printf %b 'a.mp4\nb.mp4\nc.mp4\n' | \
while read i; do
j="`basename $i .mp4`.avi"
ffmpeg -i $i $j
done
実行したところ、"a.avi"は作成されますが、"b.avi"と"c.avi"は作成されません。
原因は、FFmpegが標準入力を読み込むためだそうです。
標準入力をリダイレクトで指定してやれば、ちゃんと動くようになります。
#!/bin/sh
# 正常に動作する
printf %b 'a.mp4\nb.mp4\nc.mp4\n' | \
while read i; do
j="`basename $i .mp4`.avi"
ffmpeg -i $i $j < /dev/null
done
このような変換ソフトで実行中に標準入力を読み込むというのは、あまり例がないため、何が悪いのかをなかなか理解できず、解決するのに相当の時間を要しました。
今回は、TeXの条件分岐で予想外の結果になり、はまった話です。
TeXは組版ソフトウェアで、数式がきれいに作成できるので、学術論文などの作成に使われています。私は、業務で使う文書は原則として全てTeXで書いています。ただし、生のTeX(plain TeX)は使いにくいので、ほとんどの方がそうするように、t私もマクロ集を加えたLaTeXを使っています。表計算が必要な場合も、テキストファイルで入力データを作成し、これをPythonのスクリプトで計算し、計算結果をLaTeXで処理して文書にしています。当サイトで公開している"kianマクロ"は、LaTeXで公文書や公用文書を作るためのマクロ集です。
問題点を理解していただくための簡単な例として、次のような内容のファイル"test1.tex"を作成します。
% test1.tex
% 予想外の結果になる
\documentclass{jsarticle}
\newcount\a\a=1
\newcount\b\b=0
\newcount\c\c=0
\begin{document}
\ifnum\a=1\b=1\else\b=2\fi% (式1)\a=1なので、\b=1になる
\ifnum\b=1\c=1\else\c=2\fi% (式2)\b=1なので、\c=1になる
c=\the\c% よって、「c=1」が表示されるはず
\end{document}
次のコマンドで"test1.pdf"を作成します。
platex test1.tex
dvipdfmx test1.dvi
できた"test1.pdf"の内容を確認すると、なぜか、次のようになっています。
c=2
この現象に遭遇したのは、もっと複雑なマクロの中だったので、どこに原因があるのかが分からず、かなりの時間をかけて悩みました。
ネットの情報を参照しつつ、上記のような単純化したファイルで試して、やっと、TeXの仕様であることに気が付きました。
TeXは先読みすることがあり、(式1)を読んだときに、次の(式2)まで読み込んでしまうそうです。すなわち、\b=0の状態で(式2)を読み込んでしまうため、\c=2になってしまうそうです。
これを防止するためには、(式1)の後ろの%を外すか、\relax又は{}を入れて、先読みが及ばないようにすることです。ただし、前者については、変な空白が入る場合があり、止めておいた方が無難です。
次のコードであれば、ちゃんとc=1になります。
% test2.tex
% 予想通りの結果になる
\documentclass{jsarticle}
\newcount\a\a=1
\newcount\b\b=0
\newcount\c\c=0
\begin{document}
\ifnum\a=1\b=1\else\b=2\fi\relax% (式1)\a=1なので、\b=1になる
\ifnum\b=1\c=1\else\c=2\fi% (式2)\b=1なので、\c=1になる
c=\the\c% よって、「c=1」が表示されるはず
\end{document}
同様の問題は、次のようなコードでも起きます。
% test3.tex
% 予想外の結果になる
\documentclass{jsarticle}
\newcount\a\a=0
\newcount\b\b=0
\begin{document}
\advance\a by 1% (式3)0に1を足して、\a=1になる
\ifnum\a=0\b=0\else\b=1\fi% (式4)\a=1なので、\b=1になる
b=\the\b% よって、「b=1」が表示されるはず
\end{document}
できた"test3.pdf"の内容を確認すると、なぜか、次のようになっています。
b=0
これも、(式3)の後に\relax又は{}を入れれば、正しい結果が得られます。
なお、以上はTeXの書式ですが、これをLaTeXの書式にすれば、\relax又は{}を入れなくても、正しい結果が得られます。
% test4.tex
% 予想通りの結果になる
\documentclass{jsarticle}
\newcounter{a}\setcounter{a}{1}
\newcounter{b}\setcounter{b}{0}
\newcounter{c}\setcounter{c}{0}
\begin{document}
\ifnum\value{a}=1\setcounter{b}{1}\else\setcounter{b}{2}\fi% (式1)\a=1なので、\b=1になる
\ifnum\value{b}=1\setcounter{c}{1}\else\setcounter{c}{2}\fi% (式2)\b=1なので、\c=1になる
c=\arabic{c}% よって、「c=1」が表示されるはず
\end{document}
LaTeXのマクロはLaTeXで書くべきだと教わったことがあったような気がしますが、こういうことかと納得しました。
以前の回でハノイの塔方式のデータのバックアップが公比1/2の等比級数に理論的背景を持っていることをご説明しました。
実際に、2年間、ハノイの塔方式でバックアップを取ってみます。
最終的に残っているバックアップは、次のとおりです。
これを見ると、1年目のバックアップが1つしか残っていませんし、2年目の12月のバックアップの割合が60%もあり、最近のデータしか残っていません。これでは、気が付かないうちにデータが損傷していたような場合に、対処が困難だと思われます。
そこで、ハノイの塔方式を一般化して、もう少し古いデータも残すことができないかを考えます。
まずはおさらいですが、ハノイの塔方式は、公比1/2の等比級数が1に収束することを利用し、バックアップ回数全体を1として、Aフォルダに1/2を、Bフォルダに1/4を、Cフォルダに1/8を…を割り当てていました。
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/512 = 1
この例では、等比級数を使って、バックアップの方式を決めましたが、実は、合計が1になるように分数の和を作れば、等比級数でなくてもバックアップの方式を作ることができます。
例えば、次の分数の和を考えます。
1/2 + 1/3 + 1/6
= 3/6 + 2/6 + 1/6
= 1
そして、"1/2"をAフォルダ、"1/3"をBフォルダ、"1/6"をCフォルダに対応させ、Aフォルダは2日に1回、Bフォルダは3日に1回、Cフォルダは6日に1回、バックアップを取ります。この分数の和は、通分すると分母が6になりますので、6回のバックアップを1セットになります。
具体的には、次のようになります。
では、次の分数の和はどうでしょうか。
2/3 + 2/6
= 4/6 + 2/6
= 1
これは次のように考えます。
1つの分数につき、分子の数だけフォルダを用意します。具体的には、"2/3"をA1フォルダとA2フォルダに、"2/6"をB1フォルダとB2フォルダに対応させ、A1フォルダとA2フォルダは3日に1回、B1フォルダとB2フォルダは6日に1回、バックアップを取ります。この分数の和も、通分すると分母が6になりますので、6回のバックアップを1セットになります。
具体的には、次のようになります。
1つの分数につき、分子の数だけフォルダを用意するので、"1/2"と"2/4"は別物だと考えます。"1/2"は、Aフォルダの1つだけを用意し、2日に1回、バックアップを取ります。"2/4"は、A1フォルダとA2フォルダの2つを用意し、それぞれ4日に1回、バックアップを取ります。
そうすると、次のような分数の和も考えられます。
1/1.5 + 2/6
= 4/6 + 2/6
= 1
"1/1.5"は、Aフォルダの1つだけを用意し、3日に2回、バックアップを取ります。そのため、次のようになります。
ここまで、分数の和からバックアップのバックアップの方式を作る方法をご説明しました。
この方法を用いて、様々な分数の和を検討しましたので、いくつかご紹介したいと思います。
まずは、真っ先に思い付いたのが、公比1/3の等比級数に用いたバックアップ方式です。
2/3 + 2/9 + 2/27 + 2/81 + 2/243 + 2/729 + 1/729 = 1
公比1/3の無限等比級数は1/2に収束しますので、全体を2倍し、分子が2になっています。
1/3 + 1/9 + 1/27 + 1/81 + 1/243 + 1/729 + … = 1/2
具体的には、次のようにバックアップを取ることになります。
最終的に残っているバックアップは、次のとおりです。
公比1/2の等比級数方式(ハノイの塔方式)と比べて、あまり状況が改善していません。
等比級数方式は、後ろの項になるに従い(フォルダ名がAからZに向かうに従い)、バックアップの間隔が指数関数的に増加するので、古いデータが残りにくいのだと思われます。
そこで、公比に相当する比率を変化させてみます。
1/2 + 2/(2×3) + 3/(2×3×4) + 4/(2×3×4×5) + 5/(2×3×4×5×6) + 1/(2×3×4×5×6) = 1
公比に相当する比率が徐々に増加していますので、等比級数方式よりも状況が悪化するように思われるかもしれませんが、そうではありません。例えば、2項目の"2/(2×3)"は、バックアップの間隔が1項目"1/2"に比べて3倍になっていますが、2つのフォルダでバックアップを残しますので、バックアップの間隔はおおよそ2/3倍にしかなっていません。
具体的には、次のようにバックアップを取ることになります。
最終的に残っているバックアップは、次のとおりです。
フォルダの個数が16個まで増えてしまいましたが、1年目のバックアップが3つ残っていますし、2年目の12月のバックアップの割合も約44%に押さえることができており、ハノイの塔方式に比べてだいぶ改善したように思います。
そこで、比率をもっと大きく変化させてみたらどうかと思い、次の分数の和を試してみました。
1/2 + 3/(2×4) + 7/(2×4×8) + 15/(2×4×8×16) + 1/(2×4×8×16) = 1
最終的に残っているバックアップは、次のとおりです。
1年目のバックアップが5つに増え、2年目の12月のバックアップの割合も約32%まで減りましたが、フォルダの個数が22個まで増えてしまいました。
最後に、暦を基準にした次の分数の和を紹介して、終わります。
6/7 + 3/(7×4) + 2/(7×4×3) + 3/(7×4×3×4) + 2/(7×4×3×4×3) + 1/(7×4×3×4×3) = 1
1項目が週に、2項目が月に、3項目が四季に、4項目が年に対応しています。ただし、このバックアップは48週周期(4×3×4週周期)で回るため、1年間で約1か月(4週間と1日)のずれが生じます。
最終的に残っているバックアップは、次のとおりです。
フォルダの個数が16個まで増えた一方で、1年目のバックアップが1つしか残っておらず、しかもそれは12月のものですし、2年目の12月のバックアップの割合が約69%もあり、当初の目的に反する結果になってしまいました。
ただし、1項目が週を基準にしていますので、1週間分のバックアップが常に残っているというメリットはあります。
前回に引き続き、高次元空間のお話しです。
ネットで「モンテカルロ法で次元の呪いを体験する」という記事(http://prunus1350.hatenablog.com/entry/2015/01/19/193002)を読みました。
高次元になると、超立方体内部の体積に比べ超球面内部の体積が極端に小さくなるため、モンテカルロ法で円周率を求めることができなくなるというのが、この記事の結論です。
面白そうなので、超立方体内部の体積に対する超球面内部の体積の比を求めるプログラムを、さっそくPythonで実装してみました。
#!/usr/bin/python3
#!/usr/bin/python3
# supervolume.py
# 超立方体内部の体積に対する超球面内部の体積の比を求めるプログラム
import sys
import random
dim = 2
if(len(sys.argv) == 2):
dim = sys.argv[1]
times = 100000000
in_sphere = 0
for i in range(times):
sq_length = 0
for d in range(int(dim)):
x = (random.random())
sq_length += x*x
if(sq_length <= 1):
in_sphere += 1
print(str(in_sphere) + '/' + str(times))
これを"supervolume.py"という名前で保存し、"chmod +x supervolume.py"を実行して実行権限を付与します。
まずは、試しに2次元で実行してみます。2次元での実行は"./supervolume.py"とするだけです。
ちょっと時間がかかりましたが、結果は"78538501/100000000"と表示されました。これは、半径1の円の4分の1の面積に相当するので、これを4倍して、円周率は3.14154004と出ました。正確な値は3.14159265…ですから、まあまあの値だと思います。
作成したプログラムがまあまあ信頼できることが分かったので、さっそく記事で試していた最高の次元である15次元で試してみます。15次元での実行は"./supervolume.py 15"とするだけです。
試してみると、1回目が"1171/100000000"、2回目が"1230/100000000"、3回目が"1192/100000000"、4回目が"1192/100000000"、5回目が"1139/100000000"でした。当たり前のことですが、乱数の自乗を次元の数だけ足すので、次元が高くなるに連れて超球面内部に当たる確率が下がっていきます。
確かに、2次元の場合に比べて15次元の場合は、1万分の1以下に減少しています。
そこで、この結果を用いて、円周率を計算してみます。超球の体積から、理論的にはπ7×7!/15!=.00001164…になるそうなので、これから逆算します。
その結果は、2回目の"1230/100000000"を用いた場合は3.16641431…、5回目の"1139/100000000"も用いた場合は3.13183570…になりました。1億回も試したためか、思ったほど結果は悪くはないようです。
そこで、さらに次元を上げて、20次元で試してみたところ、1回目が"4/100000000"、2回目が"1/100000000"、3回目が"3/100000000"、4回目が"2/100000000"、5回目が"3/100000000"でした。確かにここまでばらつきが大きいと、まともに円周率は求められないと思われます。
確かに、モンテカルロ法を使って高次元空間の超球面内部の体積を求め、円周率を求めるのは難しいようです。
ネットで「高次元空間中の正規分布は超球面状に分布する」という記事(https://qiita.com/ae14watanabe/items/ef5689d40a0fbee957ea)を読みました。
正規分布は中央に山があり山から離れるほど値が小さくなるので、高次元空間になった場合でも、直感的に超球面の内部に分布しそうですが、実際には超球面の表面に分布するというのが、この記事の結論です。
そこで、なぜそうなるのかを、ちょっと考えてみることにします。
次の正規分布(標準正規分布)で2次元を考えます。
f(x) = 1/√(2π)×exp(-x2/2)
2次元では次のようになります。
f(x,y) = 1/(2π)×exp(-(x2+y2)/2)
これを極座標表示(r,θ)にすると、次のようになります。
f(r,θ) = 1/(2π)×exp(-r2/2)
θ方向に1周積分します。
f(r) = ∫02π f(r,θ) rdθ = ∫02π 1/(2π)×exp(-r2/2) rdθ = r×exp(-r2/2)
これがr一定の確率密度です。
これの増減を見るために、rで微分します。
f'(r) = (1-r2)×exp(-r2/2)
増減表は次のようになります。
| r | 0 | … | 1 | … | ∞ |
| f'(r) | 1 | + | 0 | - | 0 |
| f(r) | 0 | ↗ | 1/√e | ↘ | 0 |
確かに、f(r)は、原点付近ではなく、r=1で最大値を取ることが分かります。
もっと高次元を考えます。正規分布を使うと計算が難しいので、次のような簡単な分布を考えます。
x=-1になる確率: 1/4
x= 0になる確率: 1/2
x= 1になる確率: 1/4
同じような分布を2つ持ってきて、(x,y)を考えます。
全部で9通りの結果が考えられますが、そのうち原点からの距離rが0となる場合は(0,0)の1通りでその確率は1/2×1/2=1/4、1となる場合は(-1,0), (1,0), (0,-1), (0,1)の4通りでその確率は1/2×1/4=1/8、√2となる場合は(-1,-1), (1,-1), (-1,1), (1,1)の4通りでその確率は1/4×1/4=1/16です。
したがって、次のようになります。
【2次元の場合】
r= 0になる確率: 1/4
r= 1になる確率: 4/8 = 1/2
r=√2になる確率: 4/16 = 1/4
次に、同じような分布を3つ持ってきて、(x,y,z)を考えます。
【3次元の場合】
r= 0になる確率: 1/8
r= 1になる確率: 6/16 = 3/8
r=√2になる確率: 12/32 = 3/8
r=√3になる確率: 8/64 = 1/8
確かに、2次元と3次元の場合ですら、すでに原点からの距離が真ん中付近の確率が最大になっています。具体的には、2次元の場合はr=1の円周上が、3次元の場合はr=1とr=√2の球面上が最大になっています。簡単に確かめられますが、正規分布の場合でもそうなります。
これを一般的に求めると、次のようになります。
【n次元の場合】
r=√iになる確率: (2i×nCi)×1/2n-i×1/4i = nCi×1/2n = n!/{(n-i)!×i!}×1/2n
ここで、2N次元の場合を考えてみます。
【2N次元の場合】
r=0になる確率: 1/22N
⋮
(N-1個)
⋮
r=√Nになる確率: 2N!/(N!×N!)×1/22N
⋮
(N-1個)
⋮
r=√(2N)になる確率: 1/22N
スターリングの近似により、十分大きなnに対してn!≃√(2πn)×(n/e)nが成り立つので、これを用いて整理すると次のようになります。
【2N次元の場合】
r=0になる確率: 1/22N
⋮
(N-1個)
⋮
r=√Nになる確率: 2N!/(N!×N!)×1/22N ≃ 1/√(πN)
⋮
(N-1個)
⋮
r=√(2N)になる確率: 1/22N
r=0とr=√(2N)になる確率は指数関数で急速に減衰するのに対し、r=√Nになる確率は無理関数でゆっくりと減衰します。
考える確率の数(半径rの種類の数)が2N+1個で、次元に比例して(N倍で)増加するため、1つの確率(r=√iになる確率)は、平均的には次元に反比例して(1/N倍で)減少することを考えれば、むしろr=√Nの超球面付近に確率が集中していっているといえます。
ただし、注意が必要です。次元を固定して考えた場合、個々の点の確率、すなわち(x1,x2,x3,…)となる確率については、原点(0,0,0,…)が最大で、原点から離れるにつれて減衰します。これは完全に直感と合致します。原点付近に濃い霧がかかっており、周辺に行くに従い晴れ上がっていくイメージです。
ところが、次元が高くなるにつれて、原点から離れるにつれて点の数が指数関数で急速に増大します。
原点から離れるにつれて減衰する個々の点の確率に、原点から離れるにつれて急速に増加する点の数を掛けあわせた結果、原点付近でも最遠部でもなく、両者の間の超球面(n次元空間中のrが一定の点の集合)の確率が最大になります。そして、その結果を無理矢理に平面に落とし込むと、ネットの記事のようなドーナツ型になります。
最後に、高次元になるにつれて確率の分布の幅が狭くなり、超球面付近のみに確率が集中する理由について考えます。同じ分布で高次元にするということは、同じ試行を繰り返すことに等しいため、偶然によるばらつきが小さくなっていきます。例えば、サイコロを6回振って、1と6が3回ずつ出ることは考えられますが、サイコロを6万回振って、1と6が3万回ずつ出ることはちょっと考えられません。サイコロを6万回振れば、全ての目がおよそ1万回くらいずつ出るはずです。このように、高次元になるにしたがい、偶然によるばらつきが小さくなり、超球面付近に確率が集中していくのです。
実は、このようなことは日常的に起こっています。例えば、プロ野球の試合です。1打席の平均打率は2割5分くらいなので、次のようになります。
1打席で安打でない確率: 3/4
1打席で安打を打つ確率: 1/4
2打席の場合と3打席の場合は、次のようになります。
【2打席の場合】
0安打の確率: 9/16
1安打の確率: 6/16
2安打の確率: 1/16
【3打席の場合】
0安打の確率: 27/64
1安打の確率: 27/64
2安打の確率: 9/64
3安打の確率: 1/64
これを一般的に求めると、次のようになります。
【n打席の場合】
i安打の確率: nCi×(3/4)n-i×(1/4)i
出塁すると打席の数が変わってしまいますが、仮に1試合を27打席だと仮定して計算してみます。四球や犠打を考慮に入れていませんので、非常に簡略化したシンプルなモデルでの計算です。
【1試合(27打席と仮定)の場合】
0安打の確率: 0.04233% ← ノーヒットトーラン
1安打の確率: 0.38098%
2安打の確率: 1.65089%
3安打の確率: 4.58581%
4安打の確率: 9.17162%
5安打の確率: 14.06316%
6安打の確率: 17.18830%
7安打の確率: 17.18830%
8安打の確率: 14.32358%
9安打の確率: 10.07956%
10安打の確率: 6.04773%
11安打の確率: 3.11550%
12安打の確率: 1.38467%
⋮
確かに、個々の打席は安打でない確率の方が高いです。しかし、試合全体を見れば、6から7安打の試合が最頻値で、4安打から9安打の試合の確率で8割を超えています。0安打、すなわちノーヒットノーラン(ただし、四球や死球を考えていないので、完全試合と区別できていません。)は、0.04233%、2362試合に1試合という低確率です。適当な計算でしたが、まあまあ感覚に合致しているのではないでしょうか?
「高次元空間中の正規分布は超球面状に分布する」というショッキングなタイトルにビックリしましたが、よくよく考えてみれば自然な結論であることが理解できました。ネットの記事に感謝です。
コンピューターを使っていると、うっかりファイルを消去してしまうことがあります。また、何らかの原因でファイルが壊れてしまい、アプリケーションソフトから開けなくなってしまうことがあります。さらに、HDD(ハードディスクドライブ)やSSD(ソリッドステートドライブ)などの補助記憶装置が故障してしまい、データが取り出せなくなることもあります。
そこで、重要なデータを扱う際は、そのようなトラブルに備えて、日頃からバックアップを取っておく必要があります。
バックアップは、たくさん取っておくことに越したことはありません。可能であれば、毎日、バックアップを取って、そのデータをすべて残しておくべきです。
しかし、バックアップを保存するメディア(HDDやSSDなど)の容量にも限りがあります。
そこで、限られたメディア容量で、要領よくバックアップを取ることを考えざるを得ません。
例えば、AからJまでの10個のフォルダを作って、次のようにバックアップを取ります。
もちろん、11日目以降は、フォルダ内の古いデータを消してから、データをコピーするようにします。
この場合、メディアの容量は、バックアップを取る必要のあるデータのサイズの約10倍も必要になります。
それでも、これだと10日前までのデータしか残りません。ファイルをうっかり削除して、気が付かないまま2週間を経過してしまった場合には、バックアップが残っていません。
そこで、毎日データを取るのではなく、月に1回にしてみます。
この場合、10か月前のデータは残りますが、3日前に作成したファイルをうっかり削除した場合には、バックアップが残っていない可能性が大きいです。
そこで、両者のバランスを考えて、限られたデータ容量の中で、昔のデータのバックアップも少し残しながら、最近のデータのバックアップを小まめに残すのが理想的です。バックアップは時間が経つにつれて価値が下がっていくので、この考え方は非常に合理的です。
具体的には、Aフォルダは非常に小まめに、Bフォルダはまあまあ小まめに、Cフォルダはちょっぴり小まめに…、Iフォルダはまあまあ希に、Jフォルダは非常に希にバックアップを取ります。
そのために、1/2の有限等比級数を考えます。
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/512
= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/256
= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/128
= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/64
= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/32
= 1/2 + 1/4 + 1/8 + 1/16 + 1/16
= 1/2 + 1/4 + 1/8 + 1/8
= 1/2 + 1/4 + 1/4
= 1/2 + 1/2
= 1
そして、"1/2"をAフォルダに、"1/4"をBフォルダに、"1/8"をCフォルダに…、"1/512"をIフォルダに、最後の"1/512"をJフォルダに対応させて考えてみます。すなわち、Aフォルダは2日に1回、Bフォルダは4日に1回、Cフォルダは8日に1回…、Iフォルダは512日に1回、Jフォルダは1024×2=512日に1回、バックアップを取ることを考えてみます。
こうすると、最も新しいデータは1日前のデータ、次に新しいデータは2日前のデータになります。その後は3ないし4日前のデータ、5ないし8日前のデータ、9ないし16日前のデータとなり、最も古いデータは255ないし512日前のデータになります。
すなわち、新しいデータはたくさん、古いデータはちょっとだけ、バックアップとして残すことができるのです。
このアイデアを思い付いたときには、素晴らしいアイデアを思い付いてしまったと興奮して、実装するShell Scriptを一気に書き上げました。
ところで、話は少し変わりますが、ハノイの塔というパズルがあります。小さな円盤を大きいものから重ねて置き、小さな円盤の上に大きな円盤が乗らないようにしながら、円盤を移動させるパズルです。その名前は、「アジアのある寺院に64枚の円盤の塔があって、昼夜を通して僧侶が円盤を移し替えており、全ての円盤の移替えが終わったときに、世界は崩壊し終焉を迎える。」という物騒な伝説に由来するそうです(ただし、最低でも5845億年はかかるそうで、しばらくは世界の終焉はなさそうです。)。下に4枚のハノイの塔の例を載せますが、詳しい移動のさせ方はWikipedia等をご覧ください。

10段のハノイの塔を考え、一番小さい円盤をA円盤、次に小さい円盤をB円盤、その次に小さい円盤をC円盤…、一番大きい円盤をJ円盤とします。また、一番左の杭をア杭、真中の杭をイ杭、一番右の杭をウ杭とし、最初はア杭にすべての円盤があります。そうすると、動かし方は次のようになります。
どこの杭に移動させるのかは置いておいて、移動させる円盤のみに注目します。
そうすると、移動させる円盤の順番は「A→B→A→C→A→B→A→D→A→B→A→C→A」になっています。
この順番、実は、先ほどのバックアップのフォルダの順番と完全に一致しています。
そこで、先ほどのバックアップ方式は「ハノイの塔方式」と呼ばれているそうです。
私が思い付いたと思ったバックアップ方式は、とっくの昔に誰かが考えていたもので、車輪の再発明に過ぎなかったというのが、この話のオチです。本当にがっかりしました…。
実は、ハノイの塔方式という名前自体は以前から知っていましたし、1/2の等比級数を利用するという理論的背景をちゃんと理解した今は趣のある名前だと思いますが、当時は円盤を動かす順番でバックアップ取る変な方式という程度の認識しかありませんでした。
ハノイの塔方式のバックアップに関する記事は、ネット上にわずかしかありません。これは、趣のある名前からちょっとややこしい理論的背景に直感的に結びつきにくいことが原因ではないかと思います。しかし、ハノイの塔方式は非常に優れたアイデアですので、その理論的背景も含めて、多くの方に広く知っていただきたく、この記事を執筆いたしました。
また、後日、改めてハノイの塔方式でバックアップを取るパッケージアプリを探しましたが、Linux上では見付けることができませんでした。もしかして需要があるのではないかと思い、作成したShell Scriptを"bera(倍良)"という名前で公開しました。
前回、端末上でCtrl-;(Ctrl(Contorl)を押しながら";"を押す。)を使えない話をしました。
確かに、通常の設定ではCtrl-;を使うことは出来ません。
しかし、";"キーはホームポジションにあり、Ctrl-;は非常に打ちやすいキー操作ですから、これを有効に使わない手はありません。
そこで、発想を転換して、以前の回で紹介した方法を使います。Ctrl-;に対応する制御文字が存在しないのであれば、Ctrl-;で別の制御文字を入力するように設定し、その制御文字に命令を割り当ててやればよいのです。
例えば、"^_"という制御文字をCtrl-;に割り当てます。なぜ、"^_"なのかの理由ですが、本来、"^_"を入力するためには、Ctrl-_(Ctrlを押しながら"_"を押す。)というキー操作をしなければなりませんが、"_"自体がShiftを押しながら"\"を押す必要があるため、Ctrl-_を入力するためには、CtrlとShiftを押しながら"\"キーを押すという複雑な操作をしなければなりません。そこで、使いにくいCtrl-_で入力される"^_"を、Ctrl-;に割り当ててやることにより、使いやすくしてやろうというわけです。
具体的には、Xtermであれば、ホームディレクトリーにある".Xresources"に次のように記載して、再起動すれば、Ctrl-;で"^_"を入力させることができます。
! ~/.Xresources
! Ctrl-;を"^_"に割り当てる設定
XTerm*VT100.translations: #override \
Ctrl<Key>;: string("0x1F")
これだけでは、Ctrl-;を使うことはできません。端末上のアプリケーションの設定で、"^_"という制御文字に、機能を割り当ててやる必要があります。
例えば、端末上のシェルにBashを使っている場合、"^_"にコマンドやファイルの補完を割り当てるには、ホームディレクトリーにある".bashrc"に次のように記載して、Bashを立ち上げます。
# ~/.bashrc
# "^_"を補完に割り当てる設定
bind '"\C-_": complete'
".Xresources"と".bashrc"をセットで設定することにより、Ctrl-;でコマンドやファイルの補完ができるようになりました。
ちなみに、割り当てることができる機能(組込みコマンド)は、次のコマンドで確認できます。なお、"bash>"はコマンドプロンプトですので、入力する必要はありません。
bash> help
また、端末上のシェルにZshを使っている場合、"^_"にコマンドやファイル補完を割り当てるには、ホームディレクトリーにある".zshrc"に次のように記載して、Zshを立ち上げます。
# ~/.zshrc
# "^_"を補完に割り当てる設定
bindkey '\C-_' complete-word
".Xresources"と".zshrc"をセットで設定することにより、Ctrl-;でコマンドやファイルの補完ができるようになりました。
ちなみに、割り当てることができる機能(widget)は、次のコマンドで確認できます。なお、"zsh>"はコマンドプロンプトですので、入力する必要はありません。
zsh> zle -al
以前の回で、Xtermなどの端末上でCtrl-g(Ctrl(Control)を押しながら"g"を押す。)で割込信号を送る話をしました。
ところが、同じ方法で設定しようとしても、Ctrl-;(Ctrlを押しながら";"を押す。)で割込信号を送ることはできません。";"キーはホームポジションにあり、これを使えると非常に便利なのに、使えないのです。今回はその理由の話です。
一般的なコンピューター内部では、データは1byteという単位で扱われています。1byteとは、8桁の2進数(8bit)で、0から255までです。このうち、後半の128番から255番は、画像のデータを記録したり日本語の文字を表したりするのに使われています。前半の0番から127番までが、アルファベットを表したりコンピューターを制御したりするのに使われ、制御文字と呼びます。
今回問題になるのは、前半のアルファベットを表したりコンピューターを制御したりする部分ですので、前半の0番から127番を一覧表にしてみました。
| キー | コード | キー | コード | キー | コード | キー | コード | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ^@ | 0000000 | 64 | @ | 1000000 | 43 | + | 0101011 | 107 | k | 1101011 |
| 1 | ^A | 0000001 | 65 | A | 1000001 | 44 | ' | 0101100 | 108 | l | 1101100 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | 45 | - | 0101101 | 109 | m | 1101101 |
| 8 | ^H | 0001000 | 72 | H | 1001000 | 46 | . | 0101110 | 110 | n | 1101110 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | 47 | / | 0101111 | 111 | o | 1101111 |
| 26 | ^Z | 0011010 | 90 | Z | 1011010 | 48 | 0 | 0110000 | 112 | p | 1110000 |
| 27 | ^[ | 0011011 | 91 | [ | 1011011 | 49 | 1 | 0110001 | 113 | q | 1110001 |
| 28 | ^\ | 0011100 | 92 | \ | 1011100 | 50 | 2 | 0110010 | 114 | r | 1110010 |
| 29 | ^] | 0011101 | 93 | ] | 1011101 | 51 | 3 | 0110011 | 115 | s | 1110011 |
| 30 | ^^ | 0011110 | 94 | ^ | 1011110 | 52 | 4 | 0110100 | 116 | t | 1110100 |
| 31 | ^_ | 0011111 | 95 | _ | 1011111 | 53 | 5 | 0110101 | 117 | u | 1110101 |
| 32 | 0100000 | 96 | ` | 1100000 | 54 | 6 | 0110110 | 118 | v | 1110110 | |
| 33 | ! | 0100001 | 97 | a | 1100001 | 55 | 7 | 0110111 | 119 | w | 1110111 |
| 34 | " | 0100010 | 98 | b | 1100010 | 56 | 8 | 0111000 | 120 | x | 1111000 |
| 35 | # | 0100011 | 99 | c | 1100011 | 57 | 9 | 0111001 | 121 | y | 1111001 |
| 36 | $ | 0100100 | 100 | d | 1100100 | 58 | : | 0111010 | 122 | z | 1111010 |
| 37 | % | 0100101 | 101 | e | 1100101 | 59 | ; | 0111011 | 123 | { | 1111011 |
| 38 | & | 0100110 | 102 | f | 1100110 | 60 | > | 0111100 | 124 | | | 1111100 |
| 39 | ' | 0100111 | 103 | g | 1100111 | 61 | = | 0111101 | 125 | } | 1111101 |
| 40 | ( | 0101000 | 104 | h | 1101000 | 62 | < | 0111110 | 126 | ~ | 1111110 |
| 41 | ) | 0101001 | 105 | i | 1101001 | 63 | ? | 0111111 | 127 | ^? | 1111111 |
| 42 | * | 0101010 | 106 | j | 1101010 | ※ 32番はスペース(半角スペース)です。 | |||||
通常の文字として入力できるのは、32番のスペースから126番のチルダまでの95文字で、その中に小文字・大文字のアルファベット、数字、記号が含まれています。アルファベットの大文字が65番という中途半端な番号から始まり、大文字と小文字の間が少し番号が飛んでいます。なぜこんなにややこしい順番になっているかについては、"A"、"a"及び"1"を切りの良い数字(コードの下4桁がいずれも0001)に配置した結果だそうです。
残りの0番から31番までと127番までの33文字は、制御文字です(薄紫色の部分です。)。制御文字というのは、ベルを鳴らしたり、改行したりする制御のための特殊な文字です。例えば、8番の"^H"には1文字戻るという制御、すなわちBackSpaceが割り当てられています。そのため、端末上でBackSpaceキーを押すと、"^H"が入力されて、直前の1文字が消えます。他にも、9番の"^I"にはTabが割り当てられています。もっとも、このような例は例外的で、多くの制御文字は元々の意味とは無関係の機能を担っており、BackSpaceやTabのように専用のキーも存在しません。
いよいよ本題に入ります。
制御文字を入れるために考えられたのが、Ctrlキーです。専用のキーがなくても、Ctrlを押しながら同時にキーを押すことで入力するわけです。
Ctrlキーは、元々、コードの7桁目の0と1を入れ替えるためのキーでした。例えば、Ctrlを押しながらHを押すと、"H"のコード1001000の7桁目の1が0になってコード0001000になるため、結果として"^H"(すなわちBackSpace)が入力され、直前の1文字が消える仕組みになっていました(もしそうであるならば、単独で"h"キーを押すと"h"、Shiftを押しながら"h"キーを押すと"H"なのだから、Ctrl-Shift-hで"^H"ではないかと思うのですが、その辺りは適当に設定されているようです。)。
2進数の7桁目は64の位ですから、Ctrlは、63番以下の文字と一緒に押すと64番ほど多い文字が、64番以上の文字と一緒に押すと64番ほど少ない文字が入力されることになります。上記の表は、分かりやすいように、64番違いの文字を隣同士に配置してあります。Ctrlを押すと、左から1番目と2番目が入れ替わり、3番目と4番目が入れ替わります、
そこで、改めて表を見ると、制御文字は最初の31文字と最後の1文字しかありません。そのため、Ctrlを押すことにより、制御文字を入力できる文字は限られてしまっています。例えば、35番の"#"のコードは0100011ですが、Ctrlにより7桁目の0を1にすると、99番の"c"のコード1100011になってしまい、制御文字を入力できません。
このように、Ctrlと同時押しで制御文字を入力できるのは、「@、AからZ、[、\、]、^、_、?」の32文字しかないため、残りの文字は、Ctrlと同時押しをしたとしても、別の通常の文字になるだけで、意味がありません。59番の";"についても、Ctrlと同時押しをしたとしても、123番の"{"にしかなりません(もっとも、Ctrl-;を押しても"{"が入力されるわけではありませんので、その辺りは適当に設定されているようです。)。Ctrl-;にはこれに対応する制御文字が存在しないのです。
端末上でCtrl-;が使えないのは、このような理由です。
なお、コンピューターの進歩に伴い、Ctrlも元々の意味を失っており、Ctrl-h(Ctrlを押しながら"h"を押す。)を押しても必ずしもBackspaceにはなるとは限りません。Windowsでは、Ctrl-hに文字列を置換するという機能が割り当てられているそうです。
今回は少し長いお話です。
普段、あらゆる文書をEmacsで書いています。Emacsで文書を書いてTeXで処理して整形したり、Emacsで数値を入力してPythonのScriptで表計算をしたりしています。TeXやPythonの方が、小回りが利いて、商用ソフトよりも使い勝手が良いからです。
Emacsをお使いの方は、背景色を黒にしている方も多いと思います。その方が目に優しいからです。また、pLaTeXやPythonのキーワードに色を付けて、見やすくしている方も多いと思います。だいたい、こんな感じでしょうか。
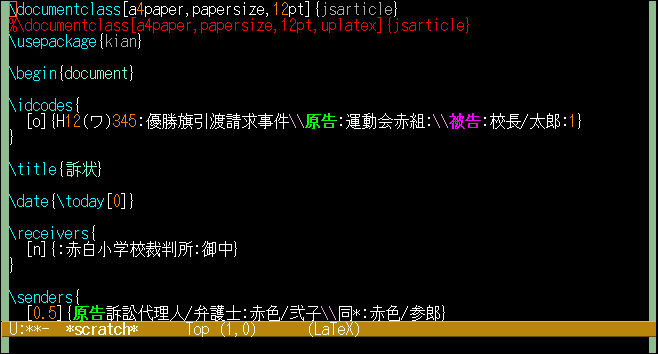
もっとも、背景色を黒にしていると、日光が当たったときに、非常に見えにくくなります。そこで、ノートパソコンを持ち歩いて使う場合などでは、背景色を白にした方が見やすいと思います。Emacsの背景色を白にしてみると、こんな感じになります。

薄い色のキーワードが目立たなくなりました。このように、キーワードの色は、背景色によって、目立ったり、目立たなくなったりします。
そこで、当初は、背景色が濃い色の場合と薄い色の場合について、それぞれキーワードの色を調合して設定していました。少しずつ色を変化させて見やすいかどうかを確認してみるという作業を繰り返すのですが、やっとできたと思った色が別の色と似ていて区別が難しかったりして、手間のかかる作業の割に納得のいく色はなかなか見つかりませんでした。
あるとき、「計算により論理的に色を調合することができないだろうか?」と思い始めました。そして、「どうせ計算するならば背景色が白でも黒でも目立つ色にして、背景色による設定を統合させたい!」と思うようになりました。以下の文章は、その試行錯誤をした結果をまとめたメモです。
一般的に色はRGBという方式で表すことが多いと思います。これは、赤(Red)、緑(Green)、青(Blue)の各色について、0から255までの数値を指定することで、色を表すものです(光の三原色は、赤黄青ではなく、赤緑青です。)。
黒:( 0, 0, 0)
赤:(255, 0, 0)
緑:( 0, 255, 0)
青:( 0, 0, 255)
白:(255, 255, 255)
この表現方式では、色は3次元直交座標系の立方体で表されることになります。
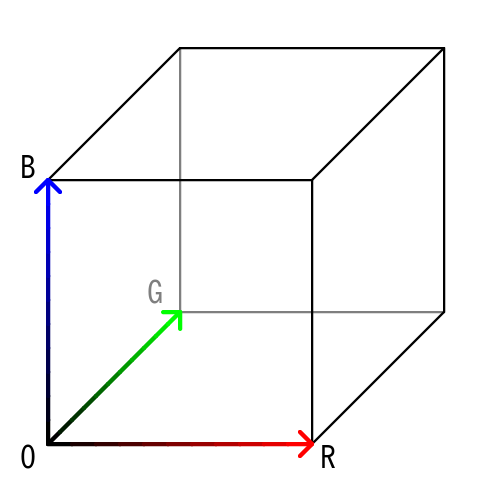
立方体の表面を着色すると、次のようになります。
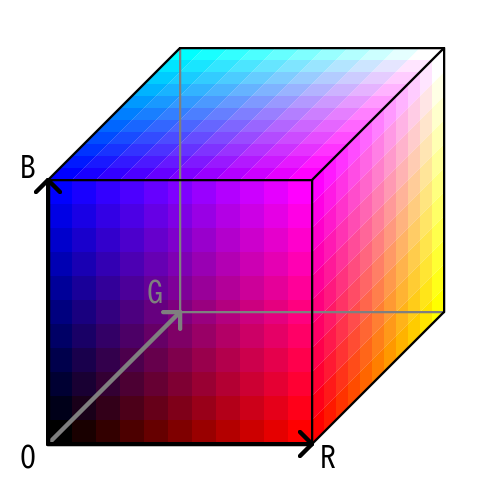
当初は、この表現形式を使い、数値を変化させて、色を作っていたのですが、なかなかうまくいきませんでした。この形式は、直感的でわかりやすいのですが、色が本来持っている性質を引き出せていないためです。
立方体を、真っ黒(0, 0, 0)から真っ白(255, 255, 255)方向(これを「BW方向」と呼ぶことにします。)に眺めると、次のように見えます(分かりやすいように、G軸とB軸を入れ替えていますが、本質的な問題ではないので、気にしないでください。)。
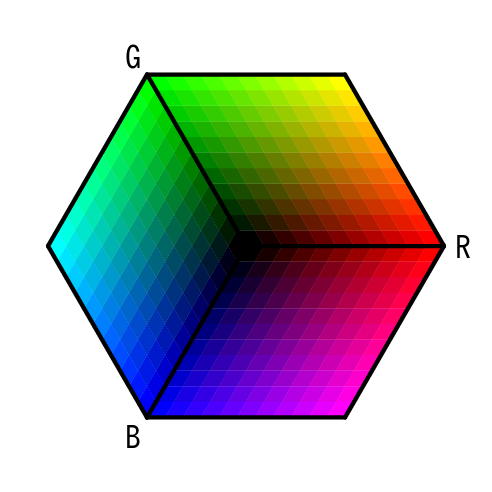
上の2つの図を眺めると、次のことがわかります。
BW方向に行くに従い、色が明るくなります。BW方向の軸(六角形の中心)から遠くに行くほど、色が鮮やかになります。BW方向の軸(六角形の中心)を中心に回転すると、色が「赤→黄→緑→シアン→青→マゼンダ→赤」と変わります。
これらを考慮し、発想を変えて、直交座標系(R,G,B)から、BW方向を高さにした円筒座標系(L,S,θ)に変換します。
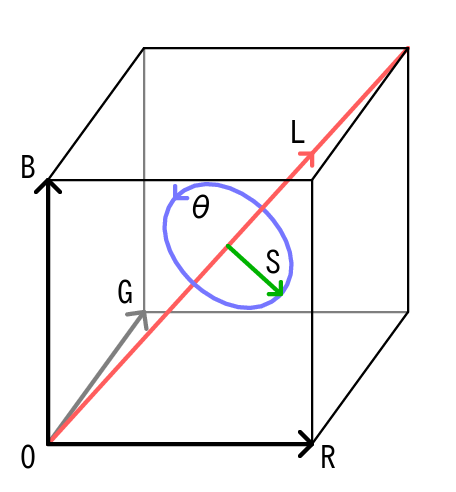
変換式は次のようになります。
L = ( √2 R + √2 G + √2 B ) / √6
x = S cosθ = ( 2 R - G - B ) / √6
y = S sinθ = ( √3 G - √3 B ) / √6
Lは明度(lightness)に由来する数値で(正確な定義は違いますが、ここでは「明度」と呼ぶことにします。)、大きいほど明るくなります(イメージは色の明るさです。)。
Sは彩度(saturation)に由来する数値で(正確な定義は違いますが、ここでは「彩度」と呼ぶことにします。)、大きいほど色が鮮やかになります(イメージは色の濁り具合です。)。
θは色相(hue)に由来する角度で、この角度が0°から360°まで変わることで、色が変わり「赤→黄→緑→シアン→青→マゼンダ→赤」の順で一周します(一言で言えば色合いです。)。この角度が同じ色は、すべて同じ色なのだけれども、明度や彩度によって見え方が違うと考えると、理解しやすいと思います。なお、角度をイメージしやすいようにθにしましたが、一般的にはHで表します。
この3つのパラメーターを色の三属性と呼ぶそうです。この3つのパラメーターに沿うように、位相幾何(トポロジー)の発想で、色相の回転を完全な円形に変形して、色空間の立方体を円錐や円柱に変形したりすることもあります。
この3つのパラメーターを使い、明度を白と黒のちょうど中間に固定して、色を調合すれば、うまくいきそうです。
ところが、これも、うまくいきませんでした。同じ明度の色でも、人間には、青は暗く見え、緑は明るく見えるため、背景色が黒の場合に青は見えにくく、背景色が白の場合に緑が見えにくくなってしまうためです。
そこで、明度Lの代わりに、輝度Yを用います。輝度は、明るさを人間の見え方に合わせて補正したもので、次の式で表されます。
Y = 0.2126 R + 0.7152 G + 0.0722 B
その結果、使う式は次の3つになります。
Y = 0.2126 R + 0.7152 G + 0.0722 B
x = S cosθ = ( 2 R - G - B ) / √6
y = S sinθ = ( √3 G - √3 B ) / √6
これを解きます。手作業でも解けなくはないですが、ちょっと面倒くさいので、PCに解かせます。
> maxima -q
(%i1) solve([ Y=0.2126*r+0.7152*g+0.0722*b, x=(2*r-g-b)/sqrt(6), y=(g-b)/sqrt(2)],[r,g,b]);
rat: replaced -0.0722 by -361/5000 = -0.0722
rat: replaced -0.7152 by -447/625 = -0.7152
rat: replaced -0.2126 by -1063/5000 = -0.2126
3937 sqrt(6) x - 3215 sqrt(2) y + 10000 Y
(%o1) [[r = -----------------------------------------,
10000
(- 1063 sqrt(6) x) + 1785 sqrt(2) y + 10000 Y
g = ---------------------------------------------,
10000
(- 1063 sqrt(6) x) - 8215 sqrt(2) y + 10000 Y
b = ---------------------------------------------]]
10000
すなわち、こうなります。
R = Y + ( 3937 √6 x - 3215 √2 y) / 10000
G = Y + (-1063 √6 x + 1785 √2 y) / 10000
B = Y + (-1063 √6 x - 8215 √2 y) / 10000
いよいよxとyを捨てて、完全に円筒座標表示にします。
R = Y + S ( 3937 √6 cosθ - 3215 √2 sinθ) / 10000
G = Y + S (-1063 √6 cosθ + 1785 √2 sinθ) / 10000
B = Y + S (-1063 √6 cosθ - 8215 √2 sinθ) / 10000
今回の目的は、①背景色が白でも黒でも目立つ②鮮やかな色を③たくさん見付けることですが、これらの性質を次のように考えます。
①背景色が白でも黒でも目立つ色というのは、黒が輝度0、白が輝度1であることに注目し、輝度Yが0.5の色と考えます。
②鮮やかな色というのは、一定の色相の中で、彩度Sが一番高い色だと考えます。
③たくさん見付けるというのは、色相の角度θについて、360度を多数に分割することにより行います。
これをPythonで実装したものが、次のコードです(コピペして実行できます。)。
#!/usr/bin/python3
# calccolors.py
# 背景色が白でも黒でも目立つ鮮やかな色をたくさん見付けるプログラム
import math
# 色をいくつ探すか
DIVISION = 12
# 輝度
LUMINANCE = 0.5
# 次の数式で、輝度、彩度及び色相から、RGB(小数表示)を計算する。
# solve([ Y=0.2126*r+0.7152*g+0.0722*b, x=(2*r-g-b)/sqrt(6), y=(g-b)/sqrt(2)],[r,g,b]);
# r = (+3937*sqrt(6)*x -3215*sqrt(2)*y +10000*Y)/10000
# g = (-1063*sqrt(6)*x +1785*sqrt(2)*y +10000*Y)/10000
# b = (-1063*sqrt(6)*x -8215*sqrt(2)*y +10000*Y)/10000
def calc_rgb_ratio(ang, lum, sat):
# 極座標表示(sat, ang)を直行座標(x, y)に変換
x = sat*math.cos(2.0*math.pi*ang/360)
y = sat*math.sin(2.0*math.pi*ang/360)
# RGB(小数表示)を求める
r_ratio = ((+ 3937*math.sqrt(6)*x - 3215*math.sqrt(2)*y) / 10000) + lum
g_ratio = ((- 1063*math.sqrt(6)*x + 1785*math.sqrt(2)*y) / 10000) + lum
b_ratio = ((- 1063*math.sqrt(6)*x - 8215*math.sqrt(2)*y) / 10000) + lum
# 結果を返す
return [r_ratio, g_ratio, b_ratio]
# 最初は彩度を大きく取り、RGB(小数表示)を計算する。
# RGB(小数表示)が0から1の範囲からはみ出しているかを確認する。
# はみ出した場合は、彩度を若干下げて、再度RGB(小数表示)を計算する。
# これを繰り返し、RGB(小数表示)がすべて0から1の範囲に収まる場合を見付ける。
# 見付かったら、その彩度とRGB(小数表示)を返す。
def get_sat_and_rgb(ang, lum):
for i in range(100000, 0, -1):
# 彩度を計算
sat = math.sqrt(3)/2*i/100000
# RGB(0〜1)を求める
rgb_ratio = calc_rgb_ratio(ang, lum, sat)
if((rgb_ratio[0] >= 0) and (rgb_ratio[0] <= 1)):
if((rgb_ratio[1] >= 0) and (rgb_ratio[1] <= 1)):
if((rgb_ratio[2] >= 0) and (rgb_ratio[2] <= 1)):
# RGB(0〜1)がいずれも0から1に収まっていれば結果を返す
return sat, rgb_ratio
# 適切な色が見付からない場合
return -1.0, [-1, -1, -1]
# 見付けた色を表示する。
def print_color(ang, lum, sat, rgb):
# 輝度
y = str(lum)
# 色相(度数法)
h = "{:03d}".format(int(ang))
# 彩度(小数点以下3桁)
s = "{0:.3f}".format(round(sat, 3))
# 色の小数表示(0〜1)
r_f = "{0:.3f}".format(round(rgb[0], 3))
g_f = "{0:.3f}".format(round(rgb[1], 3))
b_f = "{0:.3f}".format(round(rgb[2], 3))
# 色の24ビット10進法表示(000〜256)
r_d = "{:03d}".format(round(rgb[0]*255))
g_d = "{:03d}".format(round(rgb[1]*255))
b_d = "{:03d}".format(round(rgb[2]*255))
# 色24ビット16進法表示(00〜FF)
r_h = "{:02X}".format(round(rgb[0]*255))
g_h = "{:02X}".format(round(rgb[1]*255))
b_h = "{:02X}".format(round(rgb[2]*255))
# 出力
print('Y=' + y + ' θ=' + h + ' S=' + s +
' f=(' + r_f + ',' + g_f + ',' + b_f + ')' +
' d=(' + r_d + ',' + g_d + ',' + b_d + ')' +
' h=(' + r_h + ',' + g_h + ',' + b_h + ')')
# メインのループ
for n in range(DIVISION):
# 色相を度数法で計算
ang = float(n)*360/DIVISION
# 彩度とRGB(0〜1)を求める
sat, rgb = get_sat_and_rgb(ang, LUMINANCE)
# 出力
print_color(ang, LUMINANCE, sat, rgb)
実行結果です。"f"は小数表示、"d"は24ビット10進法表示、"h"は24ビット16進法表示です。
> ./calccolors.py
Y=0.5 θ=000 S=0.518 f=(1.000,0.365,0.365) d=(255,093,093) h=(FF,5D,5D)
Y=0.5 θ=030 S=0.620 f=(0.877,0.438,0.000) d=(224,112,000) h=(E0,70,00)
Y=0.5 θ=060 S=0.440 f=(0.539,0.539,0.000) d=(137,137,000) h=(89,89,00)
Y=0.5 θ=090 S=0.430 f=(0.304,0.609,0.000) d=(078,155,000) h=(4E,9B,00)
Y=0.5 θ=120 S=0.571 f=(0.000,0.699,0.000) d=(000,178,000) h=(00,B2,00)
Y=0.5 θ=150 S=0.471 f=(0.000,0.666,0.333) d=(000,170,085) h=(00,AA,55)
Y=0.5 θ=180 S=0.518 f=(0.000,0.635,0.635) d=(000,162,162) h=(00,A2,A2)
Y=0.5 θ=210 S=0.620 f=(0.123,0.562,1.000) d=(031,143,255) h=(1F,8F,FF)
Y=0.5 θ=240 S=0.440 f=(0.461,0.461,1.000) d=(118,118,255) h=(76,76,FF)
Y=0.5 θ=270 S=0.430 f=(0.696,0.391,1.000) d=(177,100,255) h=(B1,64,FF)
Y=0.5 θ=300 S=0.571 f=(1.000,0.301,1.000) d=(255,077,255) h=(FF,4D,FF)
Y=0.5 θ=330 S=0.471 f=(1.000,0.334,0.667) d=(255,085,170) h=(FF,55,AA)
この結果を帯にしてみました。

試しにグレースケールに変換してみます。

グレースケールは輝度を基準にして変換するので、すべての色が同じグレーになっています。
Emacsの設定は次のようになります。これを"colorful.el"という名前で保存して、emacsで読み込むと、"000"などのキーワードに色が付きます(目立ちやすいようにボールドにしています。)。
;;; colorful.el
(define-minor-mode angle-face-mode
"" nil " a" nil
(font-lock-add-keywords nil angle-terms)
)
(defvar angle-terms
'(("000" . angle-face-000)
("030" . angle-face-030)
("060" . angle-face-060)
("090" . angle-face-090)
("120" . angle-face-120)
("150" . angle-face-150)
("180" . angle-face-180)
("210" . angle-face-210)
("240" . angle-face-240)
("270" . angle-face-270)
("300" . angle-face-300)
("330" . angle-face-330)
))
(defface angle-face-000 '((t :foreground "rgb:FF/5D/5D" :bold t)) nil)
(defface angle-face-030 '((t :foreground "rgb:E0/70/00" :bold t)) nil)
(defface angle-face-060 '((t :foreground "rgb:89/89/00" :bold t)) nil)
(defface angle-face-090 '((t :foreground "rgb:4E/9B/00" :bold t)) nil)
(defface angle-face-120 '((t :foreground "rgb:00/B2/00" :bold t)) nil)
(defface angle-face-150 '((t :foreground "rgb:00/AA/55" :bold t)) nil)
(defface angle-face-180 '((t :foreground "rgb:00/A2/A2" :bold t)) nil)
(defface angle-face-210 '((t :foreground "rgb:1F/8F/FF" :bold t)) nil)
(defface angle-face-240 '((t :foreground "rgb:76/76/FF" :bold t)) nil)
(defface angle-face-270 '((t :foreground "rgb:B1/64/FF" :bold t)) nil)
(defface angle-face-300 '((t :foreground "rgb:FF/4D/FF" :bold t)) nil)
(defface angle-face-330 '((t :foreground "rgb:FF/55/AA" :bold t)) nil)
(defvar angle-face-000 'angle-face-000)
(defvar angle-face-030 'angle-face-030)
(defvar angle-face-060 'angle-face-060)
(defvar angle-face-090 'angle-face-090)
(defvar angle-face-120 'angle-face-120)
(defvar angle-face-150 'angle-face-150)
(defvar angle-face-180 'angle-face-180)
(defvar angle-face-210 'angle-face-210)
(defvar angle-face-240 'angle-face-240)
(defvar angle-face-270 'angle-face-270)
(defvar angle-face-300 'angle-face-300)
(defvar angle-face-330 'angle-face-330)
(angle-face-mode)
実際に試すとこうなります。


冒頭と同じ文章で試してみました。一部のキーワードを、あえてボールドにしておりませんが、ボールドにすると、もっと目立つようになると思います。

後日談ですが、キーワードをもっと目立たせたい欲望に負けてしまい、現在は、輝度が0.6の色のセットと0.4の色のセットを作り、前者を背景色が濃い色の場合に、後者を背景色が薄い色の場合に使っております(普段、背景色を"Dark Green"(輝度0.28)にしており、輝度が0.5だとキーワードが目立ちにくいのも、設定を分けた理由の1つです。)。
また、色の数も12色では少し足りないため(もう少し黄色系の色を欲しいです。)、色相をさらに分割して24色で使っています。
背景色が濃い色の場合と薄い色の場合の設定を統合するという目的には失敗しましたが、色を計算により論理的に調合するという目的は達成できたと思います。
使っているEmacs Lispを"kaki(牡蠣)"という名前で公開しました。
先日は、Kinput2で日本語入力終了キーを割り当てられない話をしました。
恥ずかしながら、あれからわずか数十日で解決いたしましたので、ご報告いたします。
失敗の原因は、開始にX Window Systemのリソースを使うため、終了もX Window Systemのリソースを使うものだと勝手に思い込んでいたことです。
Kinput2はX Window System上のアプリケーションであるため、その開始はX Window Systemのリソースを使う必要があります。しかし、一度開始してしまえば終了するのはKinput2の自由ですから、その終了はX Window Systemのリソースを使う必要はありません。すなわち、Kinput2の側で終了の設定をしてやればよいのです。
この設定は"/etc/kinput2"にある"ccdef.kinput2"又は"ccdef.kinput2.egg"で行います。私はEggユーザーですので、今回は"ccdef.kinput2.egg"に、元々設定されているShift-space(Shiftを押しながらspaceを押す。)に加えて"半角/全角"キーを日本語入力終了キーに追加する設定してみます。なお、Eggが何かについては、前回を参照してください。
"ccdef.kinput2.egg"に次のように記載して再起動すれば、Kinput2で"半角/全角"キーを日本語入力終了キーに割り当てることができます。
# /etc/kinput2/ccdef.kinput2.egg
# 日本語入力終了キーを、Shift-spaceと"半角/全角"キーに割り当てた設定
# この設定で解決
...
mode All "?"
...
"" shift-space "" end-conversion goto Hiragana
"" Zenkaku_Hankaku "" end-conversion goto Hiragana
...
endmode
最初に挑戦して失敗した1998年頃から20年以上の時を経て、あまりにも簡単に解決してしまいました。
Kinput2の開発者の皆様、誤解を招く記事を書いてしまい、申し訳ございませんでした。お詫び申し上げます。
ちなみに、ホームディレクトリーにある".Xresources"に次のように記載して再起動すれば、Kinput2で"半角/全角"キーを日本語入力開始キーに割り当てることができます。
! ~/.Xresources
! 日本語入力開始キーを、Shift-spaceと"半角/全角"キーに割り当てる設定
! この設定で解決
Kinput2*ConversionStartKeys: \
Shift<Key>space \n\
<Key>Zenkaku_Hankaku
前回は、Mode_switchの利点を解説し、Ctrl(Control)よりも活用されるべきと説明しました。
前回の設定方法("xmodmap -e 'keycode 41 = f F Right Right'"を実行)により、ほとんどのアプリではmod-f(Mode_switchを押しながら"f"を押す。)でカーソルが右に移動するようになります。しかし、ウィンドウマネージャなどのシステムに近いアプリには、前回の設定方法は効きません。X Window System上の日本語入力アプリであるKinput2も、前回の設定方法が効かないアプリの1つです。今回は、Kinput2でMode_switchを使って、mod-fでカーソルが右に移動するように設定する方法を説明します。
Kinput2のキー設定は"/etc/kinput2"にある"ccdef.kinput2"又は"ccdef.kinput2.egg"で行います。私はEggユーザーですので、今回は"ccdef.kinput2.egg"で設定してみます。ちなみに、Eggというのは、Mule(Emacsの多言語拡張版のことで、本家Emacsに統合されたため、開発は終了しています。)の日本語システムで、「"た"くさん、"ま"たせて、"ご"めんなさい」の略である"たまご"を英語化したものです。
まず、"ccdef.kinput2.egg"をEmacsやViなどのエディターで開きます。設定を見るだけであれば、一般ユーザー権限で良いですが、編集する場合は、管理者(root)権限で開く必要があります。
少し眺めてみると、モードごとにキー設定が分かれていることが分かります。今回はすべてのモード共通で設定しますので、"mode All"以下を設定します。"mode All"はファイルの最後にありますので、移動します。次のような感じになっています。
# /etc/kinput2/ccdef.kinput2.egg
...
mode All "?"
"" ' ' "" convert-next-or-move-top-or-sendback
"" '^\\' "" end-conversion goto Hiragana
"" '^@' "" convert-or-fix1
"" '^A' "" move-top
"" '^B' "" backward
"" '^C' "" clear-or-cancel
...
よく見てみると、Ctrl-f(Ctrlを押しながら"f"を押す。)の設定があり、次のようになっています。
"" '^F' "" forward
1番目の項目は前に入力されている文字、2番目の項目はキーの名前、3番目の項目は入力される文字、4番目の項目は発生する効果です。Ctrl-fの行について説明すると、1番目の項目は、入力されている文字に依存せずにカーソルが右に移動して欲しいので、空になっています。2番目の項目は、Ctrl-fのキャレット記法(caret notation)である"^F"になっています。3番目の項目は、入力される文字は不要ですので、空になっています。4番目の項目は、カーソルの右移動である"forward"になっています。
今回は、2番目の項目をmod-fになるように設定すれば良さそうです。その設定の仕方ですが、"ccdef.kinput2.egg"の下の方をよく見ると、参考になりそうな行があり、次のようになっています。
"" mod1-i "" shrink-s
xmodmap -pmを実行すると、Mode_switchはmod5に分類されているので、mod5-fとすれば良さそうです。
> xmodmap -pm
xmodmap: up to 4 keys per modifier, (keycodes in parentheses):
shift Shift_L (0x32)
lock Zenkaku_Hankaku (0x64)
control Control_L (0x17), Control_R (0x69)
mod1 Alt_L (0x40), Meta_L (0xcd)
mod2 Num_Lock (0x4d)
mod3
mod4 Super_L (0x66), Super_R (0x86), Super_L (0xce), Hyper_L (0xcf)
mod5 ISO_Level3_Shift (0x5c), Mode_switch (0xcb)
そこで、mod5-fをforwardに設定してみます。
# /etc/kinput2/ccdef.kinput2.egg
# 失敗例
...
mode All "?"
...
"" mod5-f "" forward
...
endmode
これで良さそうに思えます。ところが、これだけでは動きません。そこで、"ccdef.kinput2.egg"の上の方をよく見ると、"mode Hiragana"に次のような行があります。
"n" '^[' "ん" add-modifier-mod1
これによれば、mod5についても、"add-modifier-mod5"の設定が必要に思えます。これに気が付くまで、相当の時間を要しました。そこで、次のように設定してみます。
# /etc/kinput2/ccdef.kinput2.egg
# 失敗例
...
mode All "?"
...
"" Mode_switch "" add-modifier-mod5
"" mod5-f "" forward
...
endmode
これで、mod-fでカーソルが右に移動するようになりました。しかし、これだと、カーソルが右に移動するたびに、Mode_switchを押し直さなければなりません。カーソルを複数回右に移動する場合は、Mode_switchを押したまま、"f"を連打したり又は押し続けたりするのが普通です。これを実現するためには、カーソルが移動した後も、mod5が残るようにしなければなりません。そこで、4番目の項目に"add-modifier-mod5"を付け加えます。紆余曲折しましたが、結論として、次のように設定すれば、Kinput2でMode_switchを使えます。
# /etc/kinput2/ccdef.kinput2.egg
# 成功例
...
mode All "?"
...
"" Mode_switch "" add-modifier-mod5
"" mod5-f "" forward add-modifier-mod5
...
endmode
これで、普通にmod-fでカーソルが右に移動するようになりました。ちょっと動作が不安定な感じもありますが、十分に使えます。
Mode_switchはUNIX系のOS(Mac、Linuxなど)で用意されている修飾キー(modifier key)です。修飾キーとは、ShiftやCtrl(Control)のように、他のキーと一緒に押すことにより、キー入力を変えるキーのことをいいます。Mode_switchは、ShiftやCtrlと違い、標準でキーが割り当てられておらず、ほとんど活用されていないようです。しかし、非常に便利なキーで、もっと活用されるべきですので、以下で説明します。
もしUNIX系OSをお持ちでXmodmapを実行できる環境にあるならば、端末上(terminal上)で"xmodmap -pke | grep ' f '"と実行してみてください。下記はその実行例ですが、おそらく"keycode 41 = f F f F"というような結果が返ってくると思います。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> xmodmap -pke | grep ' f '
keycode 41 = f F f F
左辺の"41"という数字はキーの番号です。"a"キーには"38"、"s"キーには"39"というように、キーごとに数字が割り当てられています。
右辺の4つの文字は次の4つを表しています。
すなわち、"f"キーを、単独で押した場合は"f"が、Shiftと一緒に押した場合は"F"が、Mode_switchと一緒に押した場合は"f"が、Mode_switch及びShiftと一緒に押した場合は"F"が入力されることになります。このようなMode_switchの性質から、Mode_switchは第二のShiftであるともいえます(本来は"ä"のようなアクセント記号付きの文字を入力するためのキーだそうです。)。もっとも、この設定のままだと、Mode_switchを押しても押さなくても入力結果が同じであるため、Mode_switchには意味がありません。
そこで、"keycode 41 = f F Right Right"となるように設定してみます。この設定は、次のように実行すればできます("~/.Xmodmap"に設定を書いてログイン時に自動で設定させたり、ファイルに設定を書いておいて"xmodmap [filename]"を実行しても設定したりすることもできます。)。
> xmodmap -e 'keycode 41 = f F Right Right'
ここに書かれている"Right"は矢印キーの右キーを意味します。すなわち、Mode_switchを押しながら"f"キーを押すと(これを「Mod-f」と書くことにします。)、矢印キーの右キーを押した場合と同じ効果を得ることができます。すなわち、BashやEmacsなどのアプリでは、Ctrl-f(Ctrlを押しながら"f"を押す。)で、カーソルが右に移動しますが、これと同じことを実現できます。
これだけであれば、わざわざMod-fを使わなくても、Ctrl-fで十分だと思われるかもしれません。しかし、Mod-fには、Ctrl-fにはない利点があります。それは、全てのアプリで機能を統一することができることです。
Ctrl-fの場合、BashやEmacsではカーソルが右に移動する機能が割り当てられていますが(「forward」の頭文字を取ったものと思います。)、FirefoxやChromeなどでは検索機能が割り当てられています(「find」の頭文字を取ったものと思います。)。同じキー操作にもかかわらず、アプリによって機能がバラバラで、統一できていないのです(FirefoxやChromeでもCtrl-fをカーソルが右に移動する機能に割り当てようとしたことがありますが、うまくいきませんでした。)。他方、Mod-fの場合、これに矢印キーの右キーそのものを割り当てるため、どのアプリでもほぼ同じ機能(カーソルを右に移動させる機能)が割り当てられることになります。
さらに、Mode_switchを使えば、マウスの移動やクリックもキーボードから行えるようにできます。すなわち、Ctrl-fでカーソルを右に移動させる感覚で、例えばMod-gでマウスを右に移動させるようにできます。
Mode_switchはCtrlの代用となり得るキーであり、しかも機能を統一できる点でCtrlよりも便利といえます。Mode_switchはもっと活用されるべきです。
"akauni(赤海胆)"ではMode_switchをCaps_Lockキーに割り当てて、様々なキー設定をしています。
※ この件は、解決しております。解決方法はこちらをご覧ください。
日本語入力は主にFreeWnnを使っています。Emacsでの日本語入力の際に、日本語変換と同時に辞書登録ができて、非常に便利だからです。
FreeWnnは主にEmacsでの日本語入力で活躍するアプリケーションですが、X Window System上のアプリケーション(メーラーやブラウザー)で日本語入力をする際は、Kinput2を使うことになります。
その設定に関し、何年かに一度、過去の失敗を忘れて、日本語入力終了キーを"半角/全角"キーに割り当てようとすることがあり、最近もそれをやりました。
ちなみに、日本語入力開始キーを"半角/全角"キーに割り当てるのは、ホームディレクトリーにある".Xresources"に次のように記載し、再起動すればできます。
! ~/.Xresources
! 日本語入力開始キーを、Shift-spaceと"半角/全角"キーに割り当てる設定
! この設定は有効
Kinput2*ConversionStartKeys: \
Shift<Key>space \n\
<Key>Zenkaku_Hankaku
このコードでは、Shift-space(Shiftを押しながらspaceを押す。)と"半角/全角"キーを、日本語入力開始キーに割り当ています。
ところが、".Xresources"に次のように記載しても、特殊な環境でない限り、日本語入力終了キーを"半角/全角"キーに割り当てることはできません。
! ~/.Xresources
! 日本語入力終了キーを、Shift-spaceと"半角/全角"キーに割り当てようとする設定
! この設定は無効
Kinput2*ConversionEndKeys: \
Shift<Key>space \n\
<Key>Zenkaku_Hankaku
Kinput2には、日本語入力終了キーを割り当てるリソースが存在しておらず、ソースコードを書き換えない限り、割り当てることはできません。"Kinput2*ConversionEndKeys"は存在するものの、特殊な環境のためのリソースのようです。Kinput2の日本語入力終了キーは、最初から用意されているShift-spaceを使うしかないようです。
最初にこれに挑戦して失敗したのは1998年頃だったと思いますが(PC-9821にFreeBSD 2.2.6をインストールして使っていました。)、恥ずかしながら、数年に一度、過去の失敗をすっかり忘れて、挑戦と失敗を繰り返しています。
Kinput2は完全に過去の遺物になっており、使っているという方はもうおられないかもしれませんが、二度と同じ失敗を繰り返さぬように、このメモを残しておきます。
もし簡単に設定できる方法をご存知の方がおられましたら、ご連絡をお待ちしております(連絡先)。
後日談ですが、解決しました。Kinput2には、日本語入力終了キーを割り当てるリソースが存在していないことは間違っていなかったのですが、全く別の方法で解決できました。解決方法はこちらです。
前回は、端末上でCtrl-g(Ctrl(Control)を押しながら"g"を押す。)で割込信号を送る方法を説明しました。
しかし、この方法で設定できるのはCtrl-gなどに限られ、"F1"などのファンクションキーを割り当てることはできません。
これを"F1"に割り当てるのに試行錯誤し、解決法を思いつくまでに約1年もかかりました。いきなり結論ですが、端末がXtermの場合、発想を転換して、ホームディレクトリーにある".Xresources"に次のように記載して、再起動すればできます。
! ~/.Xresources
! "F1"をCtrl-cに割り当てる設定
XTerm*VT100.translations: #override \
<Key>F1: string("0x03")
上のコード中の"0x03"はキーコードを16進数で表記したもので(最初の2文字の"0x"が16進数であることを示しています。)、Ctrl-cを意味しています(正確にはキャレット記法で制御文字の"^c"を意味しています)。一方、"0x43"で"C"を意味します。"0x03"は2進数で"0000011"、"0x43"は2進数で"1000011"です。Ctrlは7ビット目(2進数の7桁目)を反転させる("0"を"1"に、"1"を"0"にする。)キーなので、"1000011"が"0000011"となるため、Ctrlを押しながら"c"を押すと、Ctrl-cという文字(割込信号)が端末に送られるのです。
もちろん、次のように実行しても構いません。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> echo 'XTerm*VT100.translations: #override <Key>F1: string("0x03")' | xrdb -merge
この設定は、Xterm上では"F1"をCtrl-cと解釈するものです(簡単に言えば、割込信号を"F1"に設定できないので、発想を転換して、"F1"を割込信号であるCtrl-cに変えているのです。)。そのため、この設定をすると、"F1"はCtrl-cと解釈され、"F1"自体を入力することができなくなります。Xterm上で動くアプリ(Emacs、W3m、Bcなど)で、"F1"をショートカットに設定していた場合、そのショートカットが使えなくなるので、注意が必要です。
あと、当たり前ですが、前回の方法でCtrl-gで割込信号を送るようにしていた場合は、上の設定では動かないので、".Xresources"に次のように記載する必要があります("0x07"でCtrl-gを意味します)。
! ~/.Xresources
! "F1"をCtrl-gに割り当てる設定
XTerm*VT100.translations: #override \
<Key>F1: string("0x07")
パソコンは、基本的にXtermを用い、CUI(Character User Interface)で使っています。CUIの方が、マウスを多用するGUI(Graphical User Interface)よりも効率がよく、履歴を確認できたり、ルーティーンワークをマクロ(Shell Script)化でできたりして、便利だからです。なお、Xtermは端末(terminal)エミュレーターの一つです。端末エミュレーターは単純に端末と呼ばれることが多いですが、UNIX系のOS(Mac、Linuxなど)でよく使う表現です。コマンドを打ち込むウィンドウのことで、WindowsでいうところのDos窓やコマンドプロンプトに相当するものになります。
端末では、割込信号を送るのに(その上で起動中のアプリを強制終了させるのに)、通常、Ctrl-c(Ctrl(Control)を押しながら"c"を押す。)を使います。
一方、文書を作成するエディターにはEmacsを用いていますが、Emacsで起動中の操作を強制終了させるのは、通常、Ctrl-g(Ctrlを押しながら"g"を押す。)であり、同じような機能であるにもかかわらず、キー操作が一致しません。
そこで、前者をCtrl-gに設定すべく試行錯誤したのですが、結論として、端末上で次を実行すればできます。なお、">"はコマンドプロンプトですので、入力する必要はありません。
> stty intr ^g
"intr"は、"interrupt"の略で、割込みを意味しています。また、"^"は慣習的にCtrlを意味しており、"^g"でCtrl-gとなりますが(厳密にはCtrl-gと"^g"は別の意味で、Ctrl-gというキー操作で"^g"という制御文字が入力されるという関係にあります。なお、"^g"は"^"と"g"の2文字ではなく、"^"が偏で"g"が旁のようなもので、これで1文字と理解します。)、このような記法をキャレット記法(caret notation)と言います。
ちなみに、端末上で次を実行すれば、現在の設定を確認できます。
> stty -a